Главная
Раздел 3. Вынужденные
колебания
3.1.
Системы с одной степенью свободы при отсутствии трения
3.1.1.Силовое
возбуждение колебаний
Независимо от
природы вынуждающих сил будем исходить из того, что каждая из них задана в виде
некоторой функции времени ![]() где
где ![]() 1,2,...,n
- порядковый номер материальной точки.
1,2,...,n
- порядковый номер материальной точки.
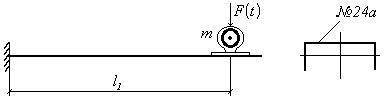
Рассмотрим
простейшую систему (рис.35,а) с одной степенью свободы, которая совершает
колебания под действием вынуждающей силы F(t). В любой
момент времени на груз массой m действуют две силы:
сила упругости пружины, пропорциональная смещению груза X, и
возмущающая сила F(t), изменяющаяся во времени по некоторому,
заранее заданному закону (рис.35,б).
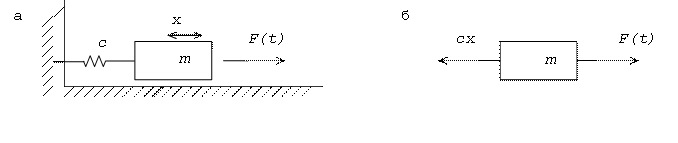
Рис. 35
Дифференциальное уравнение движения груза:
![]()
где С - жесткость пружины,
или
![]() (81)
(81)
Это уравнение иногда называют стандартным, так как к нему можно прийти и при рассмотрении других систем с одной степенью свободы, имеющих совершенно иной конструктивный вид.
В качестве
примера рассмотрим задачу о колебаниях, вызываемых единичным толчком, т.е.
внезапно приложенной в момент времени ![]() и затем постоянно
действующей силой F = 1
(рис. 36,а).
и затем постоянно
действующей силой F = 1
(рис. 36,а).
При ![]() дифференциальное
уравнение движения имеет вид
дифференциальное
уравнение движения имеет вид
![]()
Решение уравнения
должно удовлетворять начальным условиям ![]() и
и ![]() при
при ![]() и представляет собой
сумму общего решения соответствующего однородного уравнения
и представляет собой
сумму общего решения соответствующего однородного уравнения
![]()
и частного
решения заданного уравнения
![]()
т.е. ![]()
Используя начальные условия, определим постоянные интегрирования С1 и С2:
![]()
и тогда
![]()
Этот закон движения
показан на рис. 36,б. Максимальное значение смещения x
составляет ![]() , т.е. в два раза превышает перемещение, вызванное
статическим действием силы F
= 1.
, т.е. в два раза превышает перемещение, вызванное
статическим действием силы F
= 1.
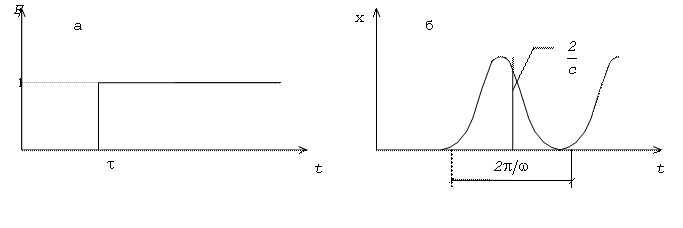
Рис. 36
3.1.2.
Кинематическое возбуждение колебаний
К такому же стандартному уравнению можно привести задачу о вынужденных колебаниях, вызываемых кинематическим способом. Рассмотрим вновь одномассовую систему, но предположим, что причиной колебаний груза m являются колебания точки крепления пружины (рис. 37). Пусть закон движения этой точки задан в виде f = f(t). Удлинение пружины в текущий момент времени равно x - f, а на груз действует сила упругости пружины - С(x - f), и дифференциальное уравнение движения
![]() ,
,
или
![]()
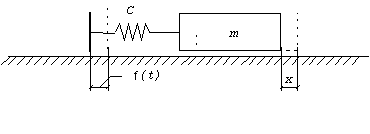
Рис. 37
Произведение Сf(t) можно считать приведенной возмущающей силой F(t), и тогда уравнение движения принимает стандартный вид (81).
3.1.3.
Общее решение стандартного уравнения
Известны несколько методов решения уравнения (81). Рассмотрим наиболее часто используемый метод - метод вариации произвольных постоянных, применение которого позволяет получить результат, пригодный для любых законов изменения возмущающей силы.
Идея метода состоит в том, что частное решение
уравнения (81) ищется в виде
![]() (82)
(82)
соответствующем решению однородного уравнения, но здесь величины С1 и С2 следует считать не постоянными, а переменными. В результате задача определения функции x(t) заменяется задачей определения двух функций - C1(t) и C2(t). Так как для этого имеется только одно уравнение (82), то функции C1(t) и C2(t) можно связать еще одной произвольной зависимостью.
Составим выражение скорости:
![]()
и свяжем ![]() и
и ![]() соотношением
соотношением
![]() (83)
(83)
тогда скорость запишется в форме
![]()
а ускорение
![]() (84)
(84)
Подставляя (82) и (84) в (81), получим
![]() (85)
(85)
Из (83) и (85) можно найти производные ![]() и
и ![]()
![]() .
.
Интегрируя,
получим
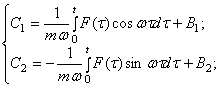 (86)
(86)
где B1 и B2 - постоянные величины.
Подставляя (86) в ( 82), получим общее решение уравнения (81)
![]() (87)
(87)
или, внося ![]() и
и ![]() под знаки интегралов и объединяя их,
под знаки интегралов и объединяя их,
![]()
Соответственно
для скорости
![]() (88)
(88)
Значения
постоянных B1
и B2 можно
определить только после того, как указаны начальные условия движения. Если ![]() при t=0, то из (87) и
(88) найдем
при t=0, то из (87) и
(88) найдем
![]()
Тогда решение
принимает вид
![]()
Здесь первые два слагаемых описывают свободные колебания, вызванные начальными возмущениями x0 и V0, а третье слагаемое характеризует вынужденные колебания, вызванные действием возмущающей силы F(t).
В случае нулевых начальных условий, когда движение начинается при x0 = 0 и V0 = 0,
![]() (89)
(89)
В некоторых случаях удобнее использовать другую форму решения, которую получим, интегрируя по частям решение (89).
Положим
![]()
Тогда
![]()
Заменяя ![]() , по формуле интегрирования по частям получим
, по формуле интегрирования по частям получим
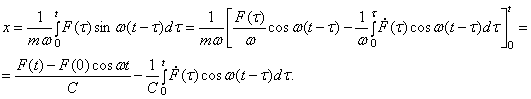 (90)
(90)
Если в
начальный момент времени F(0)=0, то
решение принимает вид
![]() (91)
(91)
где ![]() - переменное
«статическое» перемещение, вычисляемое в предположении, что силы инерции отсутствуют.
- переменное
«статическое» перемещение, вычисляемое в предположении, что силы инерции отсутствуют.
Применим
полученные результаты к случаю кинематического возбуждения колебаний (рис.37).
Полагая F(t)=Cf(t), основное решение (89) запишем в виде
![]()
Аналогично вместо формулы (90) при F(0)=0 получим
![]() (92)
(92)
3.1.4.
Действие непериодической возмущающей силы
1. Действие линейно возрастающей силы
(рис.38,а)
Используем
выражение (91), полагая ![]()
![]()
График этого движения показан на рис.38,б.
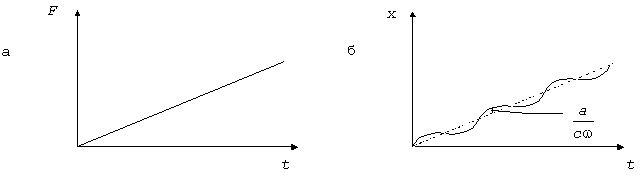
Рис. 38
Перемещения
нарастают по сложному закону, представляющему собой сумму синусоиды и линейной
функции. Дополнительное синусоидальное колебание тем существеннее, чем быстрее
нарастает сила F, т.е.
чем больше а.
Колебания подрессоренного груза при движении
по неровной дороге (рис.39)
Пусть профиль дороги задан уравнением
![]() =h(1-
=h(1-![]() ),
),
где h - предел, к которому
стремится высота профиля; ![]() - параметр, характеризующий кривизну профиля.
- параметр, характеризующий кривизну профиля.
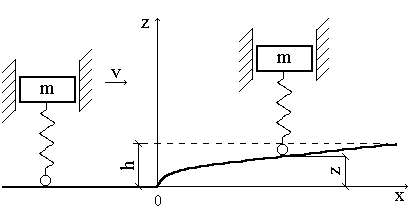
Рис. 39
Обозначим через V скорость движения груза массой m и примем начало отсчёта времени в мгновение, когда опорная точка проходит начало неровности. Тогда х=Vt и движение опорной точки по вертикали определяется законом
![]() ).
).
Дифференцируя, находим
![]() .
.
На основании (92) получим закон движения груза по вертикали:
![]() .
.
Так как
важным является не абсолютное изменение положения груза, а его колебания относительно
опорной точки, то рассмотрим разность, определяющую дополнительную деформацию
пружины![]()
![]()
![]() .
.![]()
Интегрируя, находим
![]() ,
,
где ![]() определяется
соотношением
определяется
соотношением
![]() .
.
Отсюда
следует, что при весьма малой скорости параметр ![]() стремится к
стремится к ![]() , а разность z-f - к нулю. Наоборот, при
весьма большой скорости (а также при весьма большом значении параметра
, а разность z-f - к нулю. Наоборот, при
весьма большой скорости (а также при весьма большом значении параметра ![]() ) параметр
) параметр![]() стремится к нулю, и
колебания приближённо описываются законом
стремится к нулю, и
колебания приближённо описываются законом
![]()
2. Действие
медленно изменяющихся сил
Рассмотрим
полученное выше решение задачи о вынужденных колебаниях (91). Первое слагаемое
представляет собой статическое отклонение, вызванное силой F(t). Второе слагаемое - это поправка к статическому отклонению,
причём эта поправка зависит от скорости изменения силы ![]() .
.
При малой скорости нарастания внешней нагрузки динамическая поправка к статическому решению относительно мала и нагружение практически можно рассматривать как статическое.
А.Н.Крылов
дал оценку динамической поправки для общего случая возмущающей силы. Если
кривая F(t) имеет один максимум
(рис.40,а), то, обозначая максимальное значение ![]() через
через![]() (рис.40,б), имеем
(рис.40,б), имеем
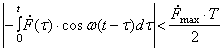 .
.
Произведение ![]() представляет собой
максимально возможное приращение возмущающей силы за промежуток времени, равный
полупериоду свободных колебаний; обозначая это произведение через
представляет собой
максимально возможное приращение возмущающей силы за промежуток времени, равный
полупериоду свободных колебаний; обозначая это произведение через ![]() Fmax,
получим
Fmax,
получим
![]() .
.
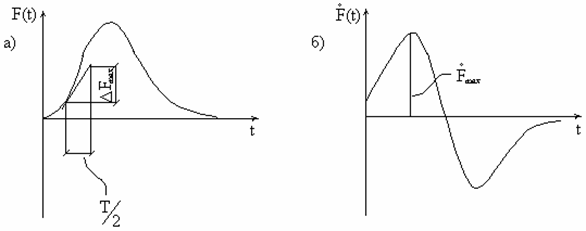
Рис. 40
Если сила
возрастает равномерно в течение времени t0, то ![]() и динамическая
"добавка" составляет
и динамическая
"добавка" составляет
![]() .
.
Её
относительная величина
![]() .
.
Отсюда следует, что если период свободных колебаний мал по сравнению с продолжительностью действия силы, то она может считаться медленно изменяющейся, а её действие можно рассчитывать без учёта динамичности, т.е. считать силу приложенной статически.
3. Действие быстро исчезающих сил
Пусть возмущающая нагрузка действует в течение весьма короткого промежутка времени. Даже значительная нагрузка может оказаться безопасной, если длительность её действия мала по сравнению с периодом свободных колебаний системы.
Рассмотрим действие силы F, которая внезапно прикладывается в момент времени t=0, действует в течение некоторого промежутка времени а, а затем также внезапно исчезает. Можно показать, что если a<T/2 , то максимальное отклонение системы достигается после исчезновения силы. В таком случае для t>à, согласно решению (89), имеем
![]() . (93)
. (93)
Обозначим
отношение промежутка времени а к
периоду свободных колебаний Т через ![]() , тогда
, тогда
![]() .
.
Максимальное отклонение в соответствии с (93):
![]() .
.
Следовательно, динамический коэффициент:
![]()
![]()
Значения
динамического коэффициента ![]() при действии силы малой продолжительности приведены в табл.
5.
при действии силы малой продолжительности приведены в табл.
5.
Таблица 5
|
|
0 |
0,01 |
0,02 |
0,03 |
0,05 |
0,10 |
0,15 |
0,25 |
0,5 |
|
|
0 |
0,062 |
0,126 |
0,188 |
0,313 |
0,618 |
0,908 |
1,413 |
2,000 |
Из приведенной таблицы видно, что если сила действует в течение малой доли периода свободных колебаний, то эффект такой кратковременной силы во много раз меньше статического. Аналогичный вывод можно сделать и в случае, когда возмущающая сила представляет собой одну половину синусоиды.
Покажем, что действие кратковременной силы приближённо можно оценить её импульсом. Для t>à решение имеет вид
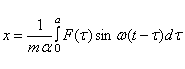 ,
,
или
![]() =
=
=![]() .
.
Но так как
отношение ![]() меньше отношения
меньше отношения![]() , то
, то ![]() есть малое число.
есть малое число.
Тогда приближённо можно записать
![]() .
.
Входящий сюда интеграл есть импульс силы F(t), т.е. движение системы определяется величиной импульса кратковременной силы, причём подробности изменения силы за промежуток времени а не играют роли.
3.1.5.
Действие гармонической силы
Случай, когда возмущающая сила изменяется по гармоническому закону
F=F0 sin pt,
(94)
где F0 - амплитуда силы; p - её частота, является наиболее распространённым в практике.
Описание колебательного процесса, вызываемого такой силой, при нулевых начальных условиях можно получить при помощи (89)
![]() . (95)
. (95)
Вычисляя
интеграл, при ![]() находим
находим
![]() .
(96)
.
(96)
Заменим ![]() и обозначим
и обозначим ![]() (прогиб, вызванный
статически приложенной постоянной силой F0, тогда
(прогиб, вызванный
статически приложенной постоянной силой F0, тогда
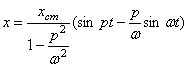 . (97)
. (97)
Из (97)
следует, что при нулевых начальных условиях возникают сложные колебания,
состоящие из двух частей: колебаний, происходящих с частотой p возмущающей силы, и колебаний,
происходящих с собственной частотой ![]() . Обычно первые колебания называют вынужденными, а вторые - свободными.
Такая терминология является условной. Дело в том, что и вторые колебания
вызваны действующей возмущающей силой, и их амплитуда зависит от этой силы; в
этом смысле вторые колебания также являются вынужденными. Указанные
наименования получили широкое распространение потому, что первое слагаемое
имеет частоту возмущающей силы, а второе меняется с собственной частотой
системы.
. Обычно первые колебания называют вынужденными, а вторые - свободными.
Такая терминология является условной. Дело в том, что и вторые колебания
вызваны действующей возмущающей силой, и их амплитуда зависит от этой силы; в
этом смысле вторые колебания также являются вынужденными. Указанные
наименования получили широкое распространение потому, что первое слагаемое
имеет частоту возмущающей силы, а второе меняется с собственной частотой
системы.
Составляющая, названная выше свободными колебаниями, быстро исчезает, поэтому достаточно ограничиться изучением стационарной, незатухающей части решения
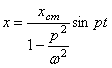 .
(98)
.
(98)
Амплитуда вынужденных колебаний
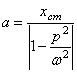 (99)
(99)
отличается от прогиба ![]() , подсчитанного в предположении статического действия силы F0. Отношение
, подсчитанного в предположении статического действия силы F0. Отношение ![]() можно назвать динамическим коэффициентом
можно назвать динамическим коэффициентом
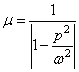 .
(100)
.
(100)
Динамический коэффициент ![]() зависит только от
отношения частот
зависит только от
отношения частот ![]() . На рис.41,a
приведена кривая зависимости
. На рис.41,a
приведена кривая зависимости![]() от отношения
от отношения ![]() .
.
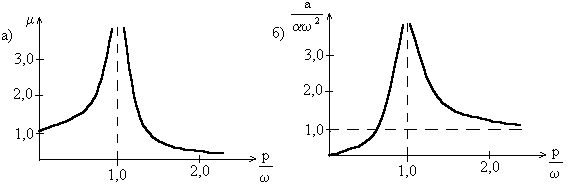
Рис. 41
При малой частоте
возмущающей силы динамический коэффициент близок к единице. С ростом частоты p динамический коэффициент
быстро увеличивается и при ![]() обращается в бесконечность. Это
соответствует состоянию резонанса, когда амплитуда вынужденных колебаний
стремится к бесконечности (если учесть силы неупругого сопротивления, то
амплитуда при резонансе окажется хотя и ограниченной, но обычно настолько
значительной, что состояние резонанса всё равно следует считать опасным).
обращается в бесконечность. Это
соответствует состоянию резонанса, когда амплитуда вынужденных колебаний
стремится к бесконечности (если учесть силы неупругого сопротивления, то
амплитуда при резонансе окажется хотя и ограниченной, но обычно настолько
значительной, что состояние резонанса всё равно следует считать опасным).
Если частота p больше собственной
частоты ![]() , то амплитуды становятся конечными; при
, то амплитуды становятся конечными; при ![]() динамический
коэффициент становится меньше единицы, т.е. динамический эффект слабее
соответствующего статического эффекта. При очень больших значениях отношения
динамический
коэффициент становится меньше единицы, т.е. динамический эффект слабее
соответствующего статического эффекта. При очень больших значениях отношения ![]() динамический
коэффициент становится весьма малым. Это означает, что сила высокой частоты не
вызывает ощутимых колебаний в упругой низкочастотной системе, которая как бы
"не успевает" отзываться на быстрые изменения возмущающей силы.
динамический
коэффициент становится весьма малым. Это означает, что сила высокой частоты не
вызывает ощутимых колебаний в упругой низкочастотной системе, которая как бы
"не успевает" отзываться на быстрые изменения возмущающей силы.
В приведенных рассуждениях считалось, что амплитудное значение возмущающей силы не связано с её частотой. Однако чаще бывает обратное, например, при вращении неуравновешенного ротора на опоры передаётся возмущающая сила
![]() ,
,
где ![]() - масса ротора; e- её эксцентриситет;
- масса ротора; e- её эксцентриситет; ![]() - угловая скорость.
- угловая скорость.
В данном
случае амплитуда возмущающей силы ![]() пропорциональна квадрату
пропорциональна квадрату ![]() , и вместо решения (96) при
, и вместо решения (96) при ![]() следует
принимать
следует
принимать
![]() .
.
Амплитуда стационарных колебаний при этом определяется выражением
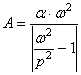 ,
,![]()
в котором
параметр системы ![]() не зависит от частоты p.
не зависит от частоты p.
На рис.41,б
представлено изменение амплитуды колебаний в зависимости от отношения ![]() .
.
Как видно,
при ![]() имеет место резонанс,
а при p»
имеет место резонанс,
а при p»![]() амплитуда стремится
к значению
амплитуда стремится
к значению ![]() .
.
Остановимся
подробнее на случае совпадения частот ![]() (резонанс).
(резонанс).
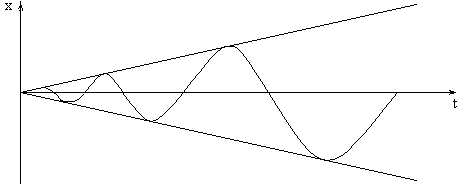
Рис. 42
При этом интеграл (95) принимает вид
![]() .
.
После вычисления получим
![]() .
.
График этого
движения показан на рис.42. Как видно, при совпадении частот амплитуда
нарастает по линейному закону и за конечный промежуток времени не обращается в
бесконечность. Из этого вытекает принципиальная возможность перехода через
резонанс, так как в процессе разгона
двигателей равенство ![]() выполняется лишь одно
мгновение и амплитуды при переходе могут не достигнуть опасных величин.
выполняется лишь одно
мгновение и амплитуды при переходе могут не достигнуть опасных величин.
3.1.6.
Действие двух гармонических сил с близкими частотами биения
Если система с одной степенью свободы испытывает действие двух различных гармонических возмущающих сил, то вследствие её линейности суммарный эффект может быть определён путём сложения эффектов, вызываемых каждой из сил. Так, возмущающая сила вида
![]()
вызовет сложные колебания
![]() . (101)
. (101)
Если частоты ![]() и
и ![]() близки одна к другой, то суммарное движение принимает
своеобразный характер и называется биением
(рис.43,a).
Особенностью биений является периодическое изменение амплитуды колебаний. Для
анализа этого явления преобразуем сначала решение (101).
близки одна к другой, то суммарное движение принимает
своеобразный характер и называется биением
(рис.43,a).
Особенностью биений является периодическое изменение амплитуды колебаний. Для
анализа этого явления преобразуем сначала решение (101).
![]()
=![]() ,
,
или
![]() , (102)
, (102)
где
![]()
![]()
Обозначая ![]() , (102) перепишем в виде
, (102) перепишем в виде
![]() .
.
Вследствие
того, что частоты ![]()
![]() близки друг другу, величины
близки друг другу, величины ![]() ,
, ![]() и
и![]() меняются медленно.
Таким образом, движение можно описать выражением
меняются медленно.
Таким образом, движение можно описать выражением
![]() ,
,
где ![]() - среднее значение частоты;
- среднее значение частоты;
![]() - медленно меняющаяся амплитуда колебаний;
- медленно меняющаяся амплитуда колебаний;
![]() - медленно
меняющаяся фаза.
- медленно
меняющаяся фаза.
Итак, движение будет носить почти синусоидальный характер, причём амплитуда колебаний А есть медленно изменяющаяся функция времени. Период изменения амплитуды А (период биений) составляет
![]() .
.
Так как
разность ![]() мала, то период ТА
значительно больше периода колебаний
мала, то период ТА
значительно больше периода колебаний
![]() .
.
Биения могут
возникнуть и при действии одной возмущающей силы ![]() вблизи резонанса,
когда частота p близка
к собственной частоте
вблизи резонанса,
когда частота p близка
к собственной частоте ![]() . Из решения (96) видно, что в данном случае колебания
состоят из двух гармоник с близкими частотами p и
. Из решения (96) видно, что в данном случае колебания
состоят из двух гармоник с близкими частотами p и ![]() . Преобразования, подобные выполненным выше, приводят к выводу, что и здесь
суммарные колебания носят синусоидальный
характер с переменной амплитудой. Однако этот процесс не является стационарным;
свободные колебания вследствие затухания постепенно исчезают, и остаются только
вынужденные колебания, так что биения прекращаются (рис.43,б).
. Преобразования, подобные выполненным выше, приводят к выводу, что и здесь
суммарные колебания носят синусоидальный
характер с переменной амплитудой. Однако этот процесс не является стационарным;
свободные колебания вследствие затухания постепенно исчезают, и остаются только
вынужденные колебания, так что биения прекращаются (рис.43,б).
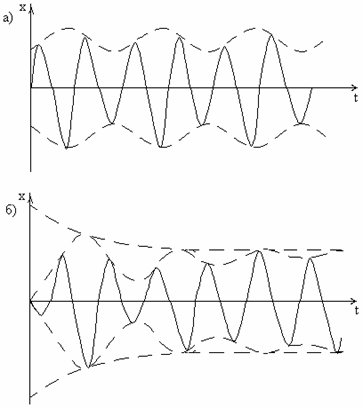
Рис. 43
3.1.7.
Действие произвольной периодической возмущающей силы (способ разложения на
гармонические составляющие)
В практических приложениях часто встречаются периодические возмущающие силы более сложного характера, чем рассмотренные выше.
Так, на рис.44,а показан закон изменения крутящего момента, создаваемого четырёхтактным двигателем внутреннего сгорания. Другой пример – периодические "безмассовые" удары – показан на рис.44,б.
Силы (моменты) рассматриваемого вида имеют чётко выраженный период колебаний Т, но не описываются единым аналитическим выражением. В подобных случаях чаще всего пользуются разложением периодической нагрузки в ряд Фурье. При этом сила представляется в виде суммы гармонических составляющих, а затем определяется эффект, вызываемый каждой из составляющих; после этого полученные частные эффекты суммируются.
Периодическую силу F(t) можно представить в виде ряда Фурье:
![]()
где ![]() - основная частота возмущения.
- основная частота возмущения.
Коэффициенты ![]() и
и
![]() вычисляются
по формулам
вычисляются
по формулам
![]()
![]()
![]()
![]()
![]()
. .
. . .
. . .
. . .
. . .
. . .
. . .
. . .
. . .
. . .
. .
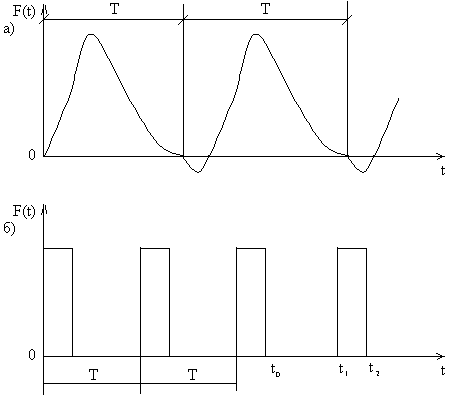
Рис. 44
Опираясь на решение (98), полученное для одной гармоники, находим
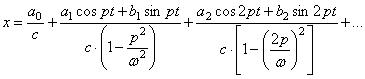 (103)
(103)
Это решение
состоит из постоянного слагаемого ![]() ,
соответствующего среднему значению возмущающей силы, и ряда, соответствующего
гармоническим колебаниям с частотами p, 2p,
.... Если собственная частота совпадает с частотой какой-либо одной гармоники np (n=1,2,...), то соответствующее слагаемое
в (103) стремится к бесконечности. Следовательно, в общем случае периодической
возмущающей силы резонанс наступает не только тогда, когда собственная частота
,
соответствующего среднему значению возмущающей силы, и ряда, соответствующего
гармоническим колебаниям с частотами p, 2p,
.... Если собственная частота совпадает с частотой какой-либо одной гармоники np (n=1,2,...), то соответствующее слагаемое
в (103) стремится к бесконечности. Следовательно, в общем случае периодической
возмущающей силы резонанс наступает не только тогда, когда собственная частота ![]() равна основной частоте возмущающей силы p, но и когда
равна основной частоте возмущающей силы p, но и когда ![]() кратно p (в некоторых частных
случаях в (103) пропадают некоторые
слагаемые, и резонанс наступает не при любой кратности).
кратно p (в некоторых частных
случаях в (103) пропадают некоторые
слагаемые, и резонанс наступает не при любой кратности).
Рассмотренный способ чётко выявляет условия наступления резонанса. Недостатком этого способа является сложность вычислений, необходимых для учёта большого числа слагаемых в (103). Так, возмущающую силу, показанную на рис.44,a, для достаточной точности необходимо заменить примерно десятью гармониками.
3.1.8.
Действие периодических импульсов
Исследуем действие периодических импульсов (рис.44,б), считая длительность каждого из них исчезающе малой.
Рассмотрим
какой-либо период Т, принимая начало
отсчёта времени в конце действия предшествующего импульса (например, в момент
времени ![]() ). Обозначим перемещение и скорость в момент времени
). Обозначим перемещение и скорость в момент времени ![]() через
через ![]() и
и ![]() .
.
В течение
рассматриваемого периода (до приложения следующего импульса) колебания являются
свободными и происходят с собственной
частотой ![]() , т.е. описываются уравнением
, т.е. описываются уравнением
![]() (104)
(104)
и, следовательно,
![]()
В конце этого
периода, непосредственно перед следующим импульсом (мгновение ![]() )
)
![]()
![]()
В результате
действия очередного импульса скорость мгновенно изменится на величину ![]() (где S - значение импульса). Поэтому
непосредственно после следующего импульса
(мгновение
(где S - значение импульса). Поэтому
непосредственно после следующего импульса
(мгновение ![]() )
)
![]()
![]()
Вследствие
периодичности процесса эти величины должны быть равны ![]() и
и ![]()
![]()
![]()
Решая
уравнения, находим ![]() и
и ![]() .
.
![]()
![]()
Закон движения (104) принимает вид
![]() (105)
(105)
Замкнутая форма этого решения позволяет легко исследовать влияние периодических ударов, в то время как способ разложения на гармонические составляющие привёл бы к бесконечным суммам.
Амплитуда колебаний определяется формулой:
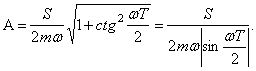
Дробь ![]() есть максимальное
отклонение, вызванное одним импульсом, поэтому выражение
есть максимальное
отклонение, вызванное одним импульсом, поэтому выражение
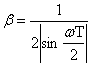
можно назвать
коэффициентом повторности. Этот
коэффициент характеризует возрастание влияния повторных импульсов. Из формулы
для величины ![]() видно, что при
совпадении частот или их кратности
видно, что при
совпадении частот или их кратности ![]()
![]()
![]() возникает резонанс.
Максимально возможное значение коэффициента повторности равно 0,5.
возникает резонанс.
Максимально возможное значение коэффициента повторности равно 0,5.
3.2. Системы
с одной степенью свободы при действии сил неупругого сопротивления
3.2.1.
Влияние вязкого трения
Общее решение. Основное уравнение вынужденных колебаний с учётом вязкого трения принимает вид
![]() (106)
(106)
где ![]()
![]()
Оно отличается от соответствующего уравнения при свободных колебаниях наличием правой части, а от уравнения вынужденных колебаний системы без трения - наличием второго слагаемого в левой части. Для получения общего решения воспользуемся способом, который применялся выше при решении подобной задачи для n = 0.
Пусть к
системе с одной степенью свободы в момент времени ![]() прикладывается
мгновенный импульс; последующий колебательный процесс можно описать уравнением
прикладывается
мгновенный импульс; последующий колебательный процесс можно описать уравнением
![]() (107)
(107)
Определим постоянные А и ![]() из условий начала
движения: при
из условий начала
движения: при ![]() должно быть Х=0,
должно быть Х=0, ![]() Первое условие даёт
Первое условие даёт
![]()
Из второго условия найдём
![]()
где ![]() .
.
Таким образом, свободные колебания, вызванные импульсом S, описываются законом
![]()
и носят затухающий характер.
Как и выше,
будем рассматривать возмущающую силу ![]() в виде
последовательности бесконечно малых импульсов
в виде
последовательности бесконечно малых импульсов ![]() . Тогда общее решение задачи о действии силы F(t) принимает вид
. Тогда общее решение задачи о действии силы F(t) принимает вид
![]() ,
(108)
,
(108)
причём закон изменения силы F(t) может быть любым.
Гармоническая возмущающая сила. В практически важном случае действия
гармонической силы ![]() решение (108) даёт
решение (108) даёт
![]() (109)
(109)
где
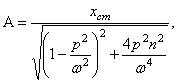 (110)
(110)
![]() (111)
(111)
![]()
Введём, как и выше, динамический коэффициент
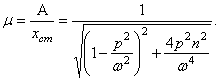 (112)
(112)
Динамический
коэффициент ![]() не обращается в
бесконечность ни при каких значениях частоты возмущения p; этим
найденный результат существенно отличается от решения, полученного выше без
учёта неупругого сопротивления. Зависимость
не обращается в
бесконечность ни при каких значениях частоты возмущения p; этим
найденный результат существенно отличается от решения, полученного выше без
учёта неупругого сопротивления. Зависимость ![]() от отношения частот
от отношения частот ![]() при различных
значениях отношения
при различных
значениях отношения ![]() приведена на рис. 45,a. Максимум динамического
коэффициента несколько смещён в сторону от абсциссы
приведена на рис. 45,a. Максимум динамического
коэффициента несколько смещён в сторону от абсциссы ![]() Однако это смещение мало, и можно приближённо
определять
Однако это смещение мало, и можно приближённо
определять ![]() подставляя в (112)
подставляя в (112) ![]() т.е.
т.е. ![]() .
.
Отсюда видно,
что максимум динамического коэффициента обратно пропорционален коэффициенту
затухания n. Из графиков (рис.45,a) следует, что силы вязкого
сопротивления оказывают заметное влияние только в околорезонансной области. Это
позволяет в удалении от резонанса принимать для ![]() кривую, построенную без учёта вязкого
сопротивления (рис. 41,a),
а во всей околорезонансной области принимать
кривую, построенную без учёта вязкого
сопротивления (рис. 41,a),
а во всей околорезонансной области принимать ![]() .
.
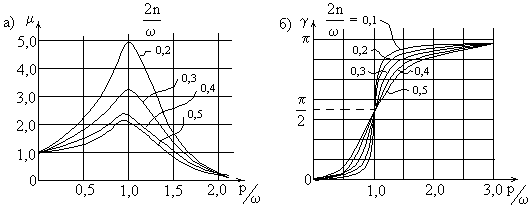
Рис. 45
Рассмотрим
вопрос о "запаздывании" колебаний. Фазовый угол ![]() определяется (111) и
зависит от отношения частот
определяется (111) и
зависит от отношения частот ![]() (рис. 45,б).
(рис. 45,б).
Как видно,
при малых частотах p
угол ![]() невелик. При резонансе
невелик. При резонансе
![]() фазовый угол равен
фазовый угол равен ![]() , т.е. в те мгновения, когда сила максимальна,
перемещение равно нулю. При высоких частотах фазовый угол близок к
, т.е. в те мгновения, когда сила максимальна,
перемещение равно нулю. При высоких частотах фазовый угол близок к ![]() ,
т.е. максимуму силы соответствует максимум перемещения.
,
т.е. максимуму силы соответствует максимум перемещения.
Действие периодических импульсов. В качестве исходного выражения примем вместо (104) закон свободных затухающих колебаний
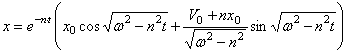 . (113)
. (113)
Дифференцируя, получим выражение скорости
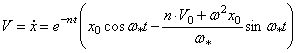 .
.
Начало
отсчёта совместим с временем ![]() (рис.44,б). Для мгновения
(рис.44,б). Для мгновения ![]() можно записать
можно записать
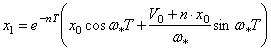 ;
;
![]()
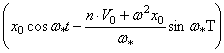 .
.
В мгновение ![]() перемещение и
скорость вновь равны
перемещение и
скорость вновь равны ![]() и
и ![]()
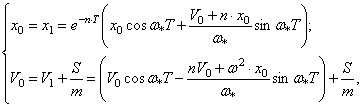 (114)
(114)
где S - величина импульса.
Из (114) находим
 (115)
(115)
Вычислив ![]() и
и ![]() , можно по (113) найти решение х.
, можно по (113) найти решение х.
Особый интерес
представляют резонансные режимы, при
которых период импульсов T
в целое число раз больше собственного периода колебаний ![]() . Обозначим это число через
. Обозначим это число через ![]() .
.
![]() .
.
Тогда
![]()
![]() ,
,
и по (115) находим
![]() ;
; ![]() .
.
При малых
значениях ![]() можно считать
можно считать
![]() т.е.
т.е. ![]() ,
,
и решение имеет вид
![]() .
.
Наибольшее значение (резонансная амплитуда) приблизительно составляет
![]() ,
,
т.е.
оказывается обратно пропорциональным коэффициенту вязкого сопротивления (как и
в случае гармонического возмущения). Коэффициент повторности при резонансе получим,
разделив ![]() на амплитуду
колебаний, вызванных однократным ударом
на амплитуду
колебаний, вызванных однократным ударом ![]() :
:
![]() ,
,
т.е. с увеличением r (уменьшением частоты импульсов) резонансные амплитуды убывают.
3.2.2.
Влияние произвольно заданных сил неупругого сопротивления
Рассмотрим
общий случай, когда сила неупругого сопротивления является некоторой нелинейной
функцией скорости: ![]() .
.
Ввиду сложности точного учёта влияния такой силы ограничимся приближённым, но дающим удовлетворительную точность простым приёмом. Заменим силу R эквивалентной силой вязкого сопротивления:
![]()
и определим
коэффициент k из
условия равенства работ, произведённых силами R и ![]() за период
колебаний.
за период
колебаний.
При этом придётся ещё ввести определённое предположение о характере колебательного процесса. При действии гармонической возмущающей силы естественно предположить, что и в общем случае сил неупругого сопротивления колебательный процесс описывается законом (109). Удобнее сместить начало отсчёта времени с таким расчётом, чтобы закон колебаний принял более простой вид
![]() (116)
(116)
и
потребовать равенства указанных работ за полупериод ![]() ), в течение которого скорость (а вместе с ней и силы
), в течение которого скорость (а вместе с ней и силы ![]() ) сохраняет постоянный знак.
) сохраняет постоянный знак.
Тогда
элементарная работа эквивалентной силы ![]()
![]() . (117)
. (117)
Подставляя
значение ![]() ,
получим
,
получим
![]()
и
соответственно этому работа силы ![]() за период равна
за период равна
![]() . (118)
. (118)
Аналогично
должна быть представлена работа, совершаемая заданной нелинейной силой
неупругого сопротивления. Положим, что указанные действия выполнены и определён
эквивалентный коэффициент ![]() (как правило, его
величина окажется зависящей от амплитуды колебаний A). Подставим найденное выражение
(как правило, его
величина окажется зависящей от амплитуды колебаний A). Подставим найденное выражение ![]() в решение (110):
в решение (110):
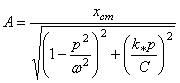 .
. ![]() (119)
(119)
Отметим, что неизвестная амплитуда A входит в обе части этого равенства. Определив из (119) зависимость амплитуды от частоты колебаний p, можем построить кривую, подобную кривым на рис. 45,а.
Проследим сказанное выше на примере сил неупругого сопротивления, заданных в виде
![]() .
(120)
.
(120)
Аналогично (117) элементарная работа силы R
![]() .
.
Если сюда подставить (116), то получим
![]() ,
,
и работа силы R за период равна
![]() .
.
Обозначим входящий в это выражение интеграл через S, тогда
![]() (121)
(121)
Приравняем (118) и (121):
![]()
Отсюда находим эквивалентный коэффициент вязкого сопротивления
![]()
который следует подставить в соотношение (119), и тогда из последнего можно определить амплитуду колебаний.
3.3. Примеры
расчётов
Пример №12. Ротор электродвигателя,
установленного на консоли (рис.46,а), имеет частоту вращения n=900 об/мин. Вследствие
неуравновешенности ротора возникает вертикальная переменная сила ![]() .Определить: 1) при каком значении
.Определить: 1) при каком значении ![]() наступает
резонанс; 2) на каком расстоянии
наступает
резонанс; 2) на каком расстоянии ![]() нужно
установить двигатель, чтобы частота собственных колебаний балки была на 30%
больше частоты возмущающей силы. Для этого случая вычислить амплитуду
вынужденных колебаний и максимальное нормальное напряжение. Массой балки
пренебречь. Масса двигателя m=100
кг; амплитуда возмущающей силы
нужно
установить двигатель, чтобы частота собственных колебаний балки была на 30%
больше частоты возмущающей силы. Для этого случая вычислить амплитуду
вынужденных колебаний и максимальное нормальное напряжение. Массой балки
пренебречь. Масса двигателя m=100
кг; амплитуда возмущающей силы ![]()
Решение
Частота возмущающей силы:
![]()
При
наступлении резонанса ![]() , т.е.
, т.е.
![]() ,
,
отсюда находим длину балки при резонансе:
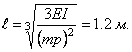
Для
выполнения условия ![]() двигатель нужно
расположить на расстоянии:
двигатель нужно
расположить на расстоянии:

Амплитуда вынужденных колебаний:
![]()
где ![]() прогиб от статического
действия силы
прогиб от статического
действия силы ![]()
Статический прогиб от собственного веса двигателя:
![]()
Статическое напряжение:
![]() .
.
Динамический коэффициент:
![]() .
.
Динамическое напряжение:
![]()
Пример 13. К валу переменного сечения с
жёстко заделанными концами прикреплён маховик, на который действует переменный
момент ![]() (рис.46,б). Определить
максимальные касательные напряжения в левой и правой частях вала, если
(рис.46,б). Определить
максимальные касательные напряжения в левой и правой частях вала, если ![]()
![]()
коэффициент сопротивления ![]()
![]() Массой вала
пренебречь.
Массой вала
пренебречь.
а
б
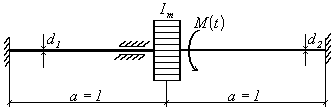
Рис. 46
Решение
Жёсткость вала:
![]()
Собственная частота колебаний:
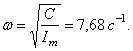
Угол поворота маховика от действия момента, равного амплитуде возмущающего момента:
![]() .
.
Амплитуда колебаний:
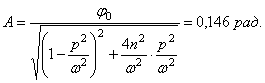
Соответствующий динамический момент:
![]()
Максимальные касательные напряжения в левой и правой частях вала:

Пример 14. Вдоль пути синусоидального
профиля ![]() (рис.47) с постоянной
горизонтальной скоростью V
движется колесо, на котором упруго подвешен груз массой m. Определить наибольшее допустимое
значение коэффициента жёсткости подвески С, если требуется, чтобы амплитуда
абсолютных колебаний груза не превышала
(рис.47) с постоянной
горизонтальной скоростью V
движется колесо, на котором упруго подвешен груз массой m. Определить наибольшее допустимое
значение коэффициента жёсткости подвески С, если требуется, чтобы амплитуда
абсолютных колебаний груза не превышала ![]() .
.
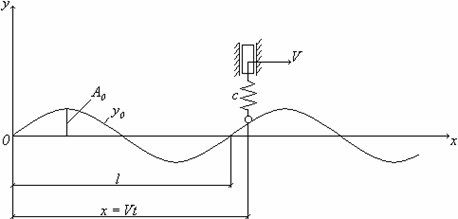
Рис. 47
Решение
Подставляя в уравнение
профиля пути ![]() , найдём ординаты нижнего конца пружины в функции времени:
, найдём ординаты нижнего конца пружины в функции времени:
![]()
Обозначая через у абсолютное вертикальное перемещение груза, отсчитываемое от равновесного уровня, дифференциальное уравнение движения запишем в виде
![]()
или
![]() .
.
Отсюда следует, что эквивалентная вынуждающая сила
![]() ,
,
т.е. её
амплитуда равна ![]() .
.
Амплитуда абсолютных колебаний груза:
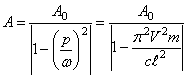 .
.
По условиям
задачи ![]() , следовательно,
, следовательно,
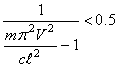 ,
,
тогда
![]() .
.
Пример 15. Двигатель весом 2,4 т
установлен на десяти одинаковых пружинах диаметром ![]() . Диаметр сечения витка пружины
. Диаметр сечения витка пружины ![]() ; модуль сдвига материала пружины
; модуль сдвига материала пружины ![]() ; частота вращения двигателя
; частота вращения двигателя ![]() . Определить число витков пружины, необходимое для того,
чтобы динамический коэффициент установки был равен 0,2.
. Определить число витков пружины, необходимое для того,
чтобы динамический коэффициент установки был равен 0,2.
Решение
Отношение 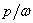 определим, используя поставленное в условиях задачи
ограничение:
определим, используя поставленное в условиях задачи
ограничение:
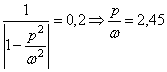 .
.
Частота возмущающей силы:
![]() .
.
Необходимое значение собственной частоты:
![]() .
.
Необходимая жёсткость всех пружин:
![]() .
.
Число витков:
![]() .
.
Следует
принять, по крайней мере, 17 витков, так как увеличение числа витков снижает
жёсткость системы и уменьшает динамический коэффициент. Если принять ![]() , то динамический коэффициент окажется больше, чем задано в
условиях задачи.
, то динамический коэффициент окажется больше, чем задано в
условиях задачи.
Пример 16. На двух балках посередине
пролёта установлен двигатель массой ![]() . Балки (двутавр №20) имеют шарнирное опирание по концам.
Ротор двигателя массой
. Балки (двутавр №20) имеют шарнирное опирание по концам.
Ротор двигателя массой ![]() имеет эксцентриситет
имеет эксцентриситет ![]() . Определить, при какой частоте вращения наступает резонанс и
чему равно при этом нормальное максимальное напряжение. Коэффициент
сопротивления
. Определить, при какой частоте вращения наступает резонанс и
чему равно при этом нормальное максимальное напряжение. Коэффициент
сопротивления ![]() ; длина пролёта
; длина пролёта ![]() ;
; ![]() . Учесть массу балок.
. Учесть массу балок.
Решение
Приведенная масса системы:
![]() ,
,
где ![]() погонная масса балки.
погонная масса балки.
Собственная частота колебаний:
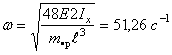 .
.
Принимая ![]() , находим частоту вращения двигателя при резонансе:
, находим частоту вращения двигателя при резонансе:
![]() .
.
Статический прогиб от амплитудного значения возмущающей нагрузки:
![]() ;
; ![]() .
.
Амплитуда колебаний:
![]() .
.
Статический прогиб:
![]() .
.
Статическое напряжение:
![]() .
.
Динамическое напряжение:
![]() .
.
3.4. Системы
с конечным числом степеней свободы(общий случай)
Способы
решения. Если внешние силы
изменяются по периодическому закону, то обычно их раскладывают в
тригонометрический ряд, т.е. представляют в виде суммы гармоник. Затем на
основании принципа независимости действия сил суммарное движение определяется
как сумма движений, вызванных каждой из гармоник в отдельности. При таком
подходе задача сводится к задаче о вынужденных колебаниях системы, вызываемых
действием одной гармоники возмущения ![]() (или
(или ![]() ), где
), где ![]() амплитуда возмущающей силы, действующей по i-му направлению;
амплитуда возмущающей силы, действующей по i-му направлению; ![]() частота возмущения, общая для всех сил, приложенных к
различным точкам системы.
частота возмущения, общая для всех сил, приложенных к
различным точкам системы.
Решение этой основной задачи чаще всего ведут одним из двух способов: непосредственного решения или разложения по собственным формам колебаний. Наибольшее распространение в расчётной практике получил второй способ. Помимо этого, иногда используется способ разложения по собственным формам колебаний при сохранении заданного вида периодических нагрузок, т.е. без разложения их на гармонические составляющие.
Особенности каждого из этих способов рассмотрим на примере простейшей двухмассовой системы (рис.48).
Непосредственное
решение. Предполагая, что внешняя нагрузка разложена в тригонометрический
ряд, исследуем движение системы, вызванное одной гармоникой возмущения. Силы,
действующие на каждую массу, обозначим через ![]() и
и ![]() . В дальнейшем будет рассмотрен также случай, когда обе силы
имеют одинаковую частоту, но разные фазы.
. В дальнейшем будет рассмотрен также случай, когда обе силы
имеют одинаковую частоту, но разные фазы.
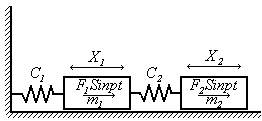
Рис. 48
Уравнения движения
такой системы аналогичны уравнениям движения при свободных колебаниях, но нули
в правых частях заменяются действующими силами ![]() и
и ![]() :
:
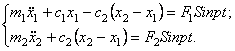 (122)
(122)
Решение этой системы, как и решение одного уравнения, состоит из двух частей: решения соответствующей однородной системы и частного решения неоднородной системы (122).
Слагаемое, описывающее колебания с собственной частотой (т.е. решение однородной системы), меняется с течением времени, быстро уменьшаясь вследствие действия сил затухания. Основной интерес представляет вторая часть решения, соответствующая незатухающему стационарному процессу вынужденных колебаний.
Примем частное решение в виде
![]() ;
; ![]() .
(123)
.
(123)
После
подстановки (123) в (122) получим два уравнения с двумя неизвестными
амплитудами ![]() и
и ![]() :
:
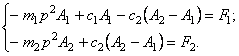 (124)
(124)
Решая систему уравнений (124), находим
 (125)
(125)
Знаменатели
выражений для ![]() и
и ![]() совпадают с левой
частью частотного уравнения (42), если заменить в нём букву
совпадают с левой
частью частотного уравнения (42), если заменить в нём букву ![]() буквой
буквой ![]() . Следовательно, если частота возмущения
. Следовательно, если частота возмущения ![]() совпадает с любой из
двух собственных частот
совпадает с любой из
двух собственных частот ![]() или
или ![]() , то знаменатели формул (125) обратятся в нуль, а амплитуды
, то знаменатели формул (125) обратятся в нуль, а амплитуды ![]() и
и ![]() станут бесконечно
большими (резонанс).
станут бесконечно
большими (резонанс).
При ![]() формулы (125)
определяют статические отклонения обеих масс,
вызванные силами
формулы (125)
определяют статические отклонения обеих масс,
вызванные силами ![]() и
и ![]() :
:
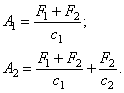
При ![]() решения системы (125)
стремятся к нулю. Зависимость амплитуды
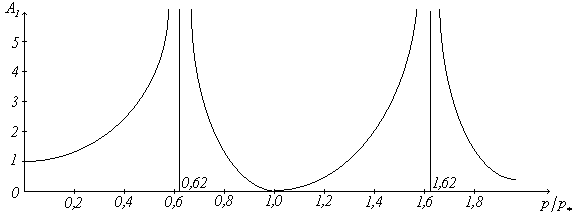
решения системы (125)
стремятся к нулю. Зависимость амплитуды ![]() от частоты показана на
рис.49. Этот график построен для случая:
от частоты показана на
рис.49. Этот график построен для случая: ![]() . В этом случае число резонансов равно двум, что
соответствует числу степеней свободы
системы и числу ее собственных частот.
. В этом случае число резонансов равно двум, что
соответствует числу степеней свободы
системы и числу ее собственных частот.
При помощи (125) можно найти форму вынужденных
колебаний, определяемую отношением ![]() к
к ![]() . В общем случае эта форма не совпадает ни с одной из
собственных форм колебаний и только при резонансах форма вынужденных колебаний
совпадает с формой свободных колебаний. Рассмотрим действие двух сил одинаковой
частоты, но сдвинутых по фазе:
. В общем случае эта форма не совпадает ни с одной из
собственных форм колебаний и только при резонансах форма вынужденных колебаний
совпадает с формой свободных колебаний. Рассмотрим действие двух сил одинаковой
частоты, но сдвинутых по фазе: ![]() и
и ![]() .
.
Эти силы можно представить в виде
![]()
а затем
решать две задачи: действуют только «синусные» составляющие ![]() и
и ![]() ; действуют только «косинусные» составляющие
; действуют только «косинусные» составляющие ![]() и
и ![]() .
.
В первой задаче получаются уравнения:
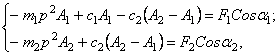
а во второй
(когда частное решение имеет вид: ![]() ;
; ![]() ):
):
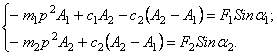
Решая каждую из этих задач и суммируя результаты, получим решение исходной задачи.
Если возмущающие силы имеют полигармоническую структуру
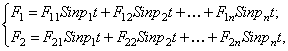
то резонанс становится возможным при
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
; ![]() ;
; ![]() ,
,
т.е. при
совпадении любой из ![]() частот возмущающей силы с любой из двух собственных частот
системы.
частот возмущающей силы с любой из двух собственных частот
системы.
Разложение решения по собственным формам колебаний
Вновь
рассмотрим простейшую систему, испытывающую действие возмущающих сил ![]() и
и ![]() .
.
Для вывода основных зависимостей рассматриваемого способа предварительно образуем вспомогательные соотношения исходя из уравнений (32). Эти уравнения удовлетворяются как решениями
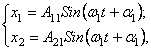 (126)
(126)
так и решениями
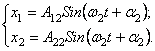 (127)
(127)
Подставляя в уравнения (32) сначала решения (126), а затем решения (127), получим две группы вспомогательных соотношений, которые будут использованы в дальнейшем
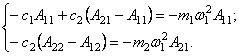 (128)
(128)
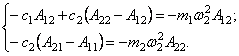 (129)
(129)
В дифференциальных уравнениях (122)
неизвестными являются функции ![]() и
и ![]() . Основная идея рассматриваемого способа состоит в замене
этих функций двумя новыми функциями
. Основная идея рассматриваемого способа состоит в замене
этих функций двумя новыми функциями ![]()
![]() такими, что
такими, что
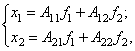 (130)
(130)
где ![]() и
и ![]() произвольные пока числа (можно, например, принять
произвольные пока числа (можно, например, принять ![]() ), с которыми
), с которыми ![]() и
и ![]() связаны известными соотношениями (собственные формы
колебаний). Подставляя (130) в (122),
получим систему дифференциальных уравнений относительно новых функций
связаны известными соотношениями (собственные формы
колебаний). Подставляя (130) в (122),
получим систему дифференциальных уравнений относительно новых функций ![]() и
и ![]() :
:
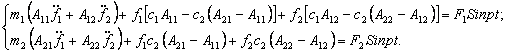 (131)
(131)
Уравнения (131) можно существенно упростить. При помощи полученных выше вспомогательных соотношений (128) и (129) перепишем (131) в виде
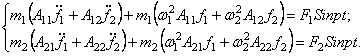 (132)
(132)
Дальнейшие
упрощения вытекают из свойств ортогональности собственных форм колебаний.
Умножим первое из уравнений (132) на ![]() ,
а второе - на
,
а второе - на ![]() и сложим их:
и сложим их:
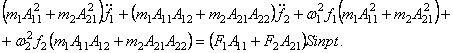
Согласно свойству ортогональности,
![]()
и из
записанного уравнения выпадают функция ![]() и её вторая производная
и её вторая производная ![]() ;
в результате получается дифференциальное уравнение, содержащее только функцию
;
в результате получается дифференциальное уравнение, содержащее только функцию ![]()
![]() (133)
(133)
Аналогично можно получить дифференциальное
уравнение, содержащее только функцию ![]() .
Для этого нужно первое из уравнений (132) умножить на
.
Для этого нужно первое из уравнений (132) умножить на ![]() ,
второе - на
,
второе - на ![]() и полученные уравнения сложить. Используя
затем то же свойство ортогональности, будем иметь
и полученные уравнения сложить. Используя
затем то же свойство ортогональности, будем иметь
![]() (134)
(134)
Таким образом, способ разложения по собственным формам колебаний приводит к раздельным уравнениям (133) и (134), каждое из которых описывает колебания некоторой системы с одной степенью свободы.
Если
обозначить правые части дифференциальных уравнений (133) и (134) соответственно
через ![]() и
и ![]() ,
где
,
где
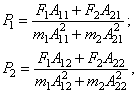
то стационарная часть решения имеет вид
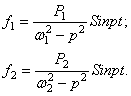
Подставляя ![]() и
и ![]() в соотношения (130), получим решения для
обобщённых координат
в соотношения (130), получим решения для
обобщённых координат ![]() и
и ![]() :
:
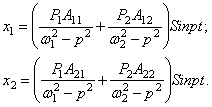
Приведенные выше действия обеспечивают разделение уравнений при любом конечном числе степеней свободы системы.
Разложение решения по собственным формам
колебаний при сохранении заданного вида периодических нагрузок
Основное
преимущество рассмотренного выше способа - разделение уравнений - никак не
связано с тем или иным конкретным видом возмущающих сил. Иначе говоря,
разделение уравнений так же легко достигается в случае произвольно заданных возмущающих
сил ![]() ,
, ![]() , как и в рассмотренном случае гармонических возмущающих сил
, как и в рассмотренном случае гармонических возмущающих сил ![]() . Не повторяя выкладок, сразу приведём окончательные
дифференциальные уравнения для общего случая
. Не повторяя выкладок, сразу приведём окончательные
дифференциальные уравнения для общего случая

Такие уравнения легко интегрируются при любом виде правых частей. Таким образом, способ разложения решения по собственным формам колебаний не требует предварительного разложения возмущающих сил на гармонические составляющие. Такое разложение является достаточно громоздкой операцией и, как правило, требует учёта большого числа гармоник. Эта операция оправдана только при решении задачи первым способом.
3.5.
Стержневые системы с конечным числом степеней свободы при гармоническом нагружении
При действии на упругую систему (балку или раму) с конечным числом степеней свободы вибрационной гармонической нагрузки изгибающие моменты, поперечные и продольные силы также будут изменяться во времени, а их наибольшие значения (амплитуды) будут зависеть от частот возмущающих сил. Если все возмущающие нагрузки, действующие на систему, имеют одну и ту же частоту р и изменяются в одной фазе, то силы инерции, а следовательно, и изгибающие моменты, поперечные и продольные силы достигают наибольших значений в одно и то же время.
Для решения задачи о вынужденных колебаниях стержневой
системы можно использовать как метод сил, так и метод перемещений, причём
наибольшее применение в расчётной практике находит первый из указанных методов.
Метод
сил. Рассмотрим упругую систему (рис.50) с конечным числом сосредоточенных
масс, на которую действуют вибрационные силы ![]() .
.
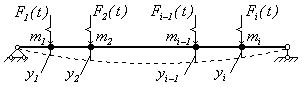
Рис. 50
Перемещение
любой массы ![]() в произвольный момент
времени
в произвольный момент
времени ![]() выражается в виде
выражается в виде
![]() ,
(135)
,
(135)
где ![]() силы инерции соответствующих масс;
силы инерции соответствующих масс; ![]() перемещения по
направлению силы инерции
перемещения по
направлению силы инерции ![]() , вызванные единичными силами
, вызванные единичными силами ![]() , приложенными в точках нахождения соответствующих масс;
, приложенными в точках нахождения соответствующих масс; ![]() перемещение точки расположения массы
перемещение точки расположения массы ![]() от действия
амплитудных значений всех приложенных
вибрационных нагрузок.
от действия
амплитудных значений всех приложенных
вибрационных нагрузок.
Перечисленные перемещения вычисляются путём перемножения соответствующих эпюр методом Мора-Верещагина.
С другой
стороны, при гармонических вынужденных колебаниях с частотой р перемещение массы ![]() и её ускорение можно
записать в виде
и её ускорение можно
записать в виде
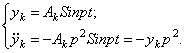
Сила инерции
массы ![]() :
:
![]() ,
,
отсюда
![]() (136)
(136)
Подставляя (136) в (135), после простейших преобразований получим
![]() ,
,
где
![]() .
.
Записывая аналогичные уравнения для каждой из сосредоточенных масс, получим систему уравнений, которая называется системой канонических уравнений динамического варианта метода сил:
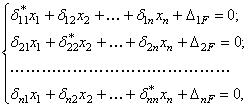 (137)
(137)
где ![]() число степеней свободы системы.
число степеней свободы системы.
Уравнения (137) позволяют определить наибольшие (амплитудные) значения сил инерции.
Сама система уравнений (137) по форме аналогична системе канонических уравнений метода сил, используемого при расчёте статически неопределимых систем, но неизвестными в ней являются не реакции отброшенных связей в статически неопределимой системе, а амплитуды сил инерции масс, которые могут возникать как в статически определимой, так и в статически неопределимой системах.
После
вычисления максимальных значений сил инерции ![]() эпюра динамических
изгибающих моментов строится путём сложения единичных эпюр, предварительно
умноженных на найденные значения соответствующих инерционных сил, с эпюрой
эпюра динамических
изгибающих моментов строится путём сложения единичных эпюр, предварительно
умноженных на найденные значения соответствующих инерционных сил, с эпюрой ![]() , т.е. в соответствии с выражением
, т.е. в соответствии с выражением
![]() .
.
Использование симметрии системы при её расчёте на вынужденные колебания оказывается возможным только при симметричном расположении масс.

Рис. 51
При несимметричной вибрационной нагрузке разложение сил инерции на симметричные и обратно симметричные группы (рис.51) приводит к распаду системы канонических уравнений на две независимые системы.
В этом случае вычисление главных перемещений по направлению парных неизвестных нужно вести по формуле
![]() .
.
При симметричной вибрационной нагрузке все обратно симметричные силы инерции равны нулю, а при обратно симметричной вибрационной нагрузке симметричные силы инерции равны нулю. Симметричная нагрузка может привести к резонансу только при совпадении её частоты с собственными частотами симметричных колебаний системы и, наоборот, обратно симметричная нагрузка может дать резонанс только с частотами обратно симметричных свободных колебаний.
Метод перемещений. Этому методу отдают
предпочтение при расчёте рам на вынужденные колебания. Рассмотрим систему
(рис.52,а), для которой основная система получается путём введения связей по
направлению неизвестных перемещений ![]() соответствующих масс
соответствующих масс ![]() (рис.52,б).
(рис.52,б).
а б
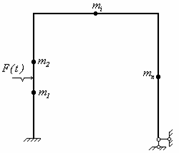
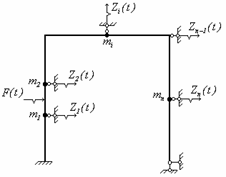
Рис. 52
Уравнение,
выражающее равенство нулю динамической реакции введённой связи по направлению
любого перемещения ![]() с учётом силы инерции
с учётом силы инерции ![]() , выражается в виде
, выражается в виде
![]() .
.
Учитывая, что
при гармонических колебаниях ![]() , получим систему уравнений
, получим систему уравнений
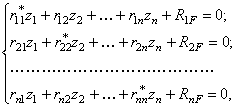 (138)
(138)
где
![]() .
.
Строго
говоря, неизвестные ![]() и свободные члены
и свободные члены ![]() являются величинами
переменными, изменяющимися одновременно и по одному и тому же закону,
характеризуемому множителем
являются величинами
переменными, изменяющимися одновременно и по одному и тому же закону,
характеризуемому множителем ![]() , к их амплитудным значениям. Так как этот множитель присутствует
во всех членах системы (138), то на него может быть произведено сокращение.
Тогда неизвестные и свободные члены уравнений (138) должны рассматриваться в
качестве соответствующих амплитудных значений.
, к их амплитудным значениям. Так как этот множитель присутствует
во всех членах системы (138), то на него может быть произведено сокращение.
Тогда неизвестные и свободные члены уравнений (138) должны рассматриваться в
качестве соответствующих амплитудных значений.
Реакции ![]() определяются от
единичных перемещений основной системы, приложенных в тех сечениях, где
находятся точечные массы, т.е. так же, как и при определении частот свободных
колебаний.
определяются от
единичных перемещений основной системы, приложенных в тех сечениях, где
находятся точечные массы, т.е. так же, как и при определении частот свободных
колебаний.
Реакции от амплитудных значений вибрационных
нагрузок ![]() определяются в
основной системе.
определяются в
основной системе.
После вычисления неизвестных амплитуд
перемещений ![]() эпюра динамических
изгибающих моментов строится в соответствии с выражением
эпюра динамических
изгибающих моментов строится в соответствии с выражением
![]() ,
,
где ![]() эпюры изгибающих
моментов в основной системе от соответствующих единичных перемещений;
эпюры изгибающих
моментов в основной системе от соответствующих единичных перемещений; ![]() эпюра моментов в основной системе от амплитудных значений
вибрационных нагрузок.
эпюра моментов в основной системе от амплитудных значений
вибрационных нагрузок.
Система
уравнений (138) по своей структуре аналогична системе канонических уравнений
метода перемещений, применяемого для расчёта статически неопределимых систем,
но здесь неизвестные ![]() являются не искомыми
перемещениями узлов рамы, а амплитудами перемещений сосредоточенных масс.
являются не искомыми
перемещениями узлов рамы, а амплитудами перемещений сосредоточенных масс.
Так же как и метод сил, метод перемещений может быть использован не только для систем, совершающих изгибные вынужденные колебания, но и для систем, испытывающих продольные вынужденные колебания.
3.6.
Крутильные колебания валов
Вынужденные колебания валов являются следствием переменности вращающих моментов, действующих на вал. Эти моменты носят периодический характер и обусловлены как давлением газа в цилиндрах, так и силами инерции движущихся частей.
Рассмотрим
наиболее общий случай, когда на отдельные диски эквивалентной системы действуют
любым образом заданные переменные моменты (рис.26,а). Средние во времени
значения этих моментов вызывают также постоянную во времени деформацию вала,
поэтому для анализа колебаний достаточно учесть влияние только переменных
частей каждого момента. Обозначим эти части через ![]() и будем называть их возмущающими моментами.
и будем называть их возмущающими моментами.
Если считать, что неупругие сопротивления отсутствуют, то уравнения вынужденных колебаний будут отличаться от уравнений свободных колебаний этой же системы наличием возмущающих моментов:
 (139)
(139)
Решение системы (139) можно получить всеми тремя
рассмотренными способами (см. подразд. 8.4).
Непосредственное решение
Для
применения первого способа необходимо предварительно разложить периодические
возмущающие моменты в ряды Фурье. После этого уравнения (139) решаются
несколько раз - отдельно для каждой гармоники возмущения. Это приводит к ряду
однотипных частных задач, каждая из которых требует анализа действия
возмущающих моментов одинаковой частоты ![]() :
:
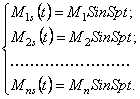 (140)
(140)
При этом стационарные колебания будут происходить с частотой возмущения:
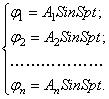 (141)
(141)
Подставляя (140) и (141) в (139), получим систему алгебраических уравнений
 (142)
(142)
Решая эту
систему, находим амплитуды вынужденных колебаний ![]() , а затем и крутящие моменты в сечениях вала:
, а затем и крутящие моменты в сечениях вала: ![]() на первом участке;
на первом участке; ![]() на втором и т.д.
на втором и т.д.
Разложение решения по собственным формам колебаний
Этот способ требует предварительного расчёта частот и форм собственных колебаний, после чего расчёт на вынужденные колебания становится сравнительно простым.
Будем
считать, что известны как собственные частоты ![]() (число собственных
частот равно
(число собственных
частот равно ![]() , а не
, а не ![]() , так как одна частота равна нулю и соответствует повороту
вала и дисков как жёсткого целого), так и соответствующие формы колебаний (т.е.
отношения между амплитудами
, так как одна частота равна нулю и соответствует повороту
вала и дисков как жёсткого целого), так и соответствующие формы колебаний (т.е.
отношения между амплитудами ![]() первой собственной
формы;
первой собственной
формы; ![]() второй собственной
формы и т.д.).
второй собственной
формы и т.д.).
Системе
уравнений (65), описывающих свободные колебания рассматриваемой системы,
удовлетворяют функции, определяющие любое ![]() главное колебание:
главное колебание:
 (143)
(143)
Подставляя (143) в систему уравнений (65), получим вспомогательные соотношения:
 (144)
(144)
Произведём
замену переменных в системе уравнений (139), введя новые функции ![]() , которые связаны с функциями
, которые связаны с функциями ![]() следующим образом:
следующим образом:
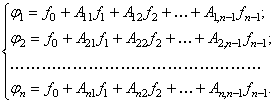 (145)
(145)
Функция ![]() , общая для всех уравнений системы (145), соответствует
вращению системы как жёсткого целого, т.е. нулевой собственной форме колебаний.
Коэффициенты первой строки
, общая для всех уравнений системы (145), соответствует
вращению системы как жёсткого целого, т.е. нулевой собственной форме колебаний.
Коэффициенты первой строки ![]() принимаются любыми
(например,
принимаются любыми
(например, ![]() ), тогда значения остальных коэффициентов определяются
соответствующими собственными формами.
), тогда значения остальных коэффициентов определяются
соответствующими собственными формами.
Подставляя (145) в систему уравнений (139), получим

Если учесть вспомогательные соотношения (144), то запись уравнений упрощается:

или после преобразований
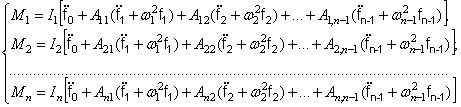 (146)
(146)
Эта система уравнений распадается на независимые уравнения, если, как и выше, воспользоваться свойством ортогональности. Сложим все уравнения (146). Тогда первые слагаемые правых частей дадут сумму:
![]()
а вторые слагаемые –
![]()
Эта сумма вторых слагаемых равна нулю, так как сумма в первой скобке обращается в нуль вследствие ортогональности первой и нулевой форм колебаний. Точно так же обращаются в нуль результаты суммирования всех следующих слагаемых, входящих в правые части уравнений (146). Поэтому после сложения всех уравнений (146) получим
![]()
Интегрируя это уравнение, можно найти функцию f0.
Затем, умножив первое из уравнений (146) на А11, второе - на А21, третье - на А31 и т.д., сложим все полученные уравнения. При этом первые слагаемые правых частей образуют произведение:
![]()
причем сумма, заключенная в скобки, равна нулю. Суммирование вторых слагаемых дает отличное от нуля выражение
![]()
При суммировании третьих слагаемых получим
![]()
Вследствие ортогональности первых двух форм колебаний сумма в первой скобке, а следовательно, и все это выражение равно нулю. Аналогично равна нулю сумма четвертых слагаемых, пятых и т.д.
Окончательно
получим дифференциальное уравнение, содержащее только одну функцию f1
![]()
Аналогично
можно получить дифференциальное уравнение для функции f2. Для этого нужно умножить
первое из уравнений (146) на А12, второе - на А22, третье
- на А32 и т.д. Последовательно применяя тот же прием, можно
образовать отдельные уравнения для остальных неизвестных функций. Для i-й функции fi дифференциальное уравнение имеет вид
![]() (147)
(147)
Уравнения этого типа наиболее удобны, так как с их помощью задача о колебаниях системы с n степенями свободы заменяется n простыми задачами о колебаниях системы с одной степенью свободы. При практическом расчете крутильных колебаний валов существенными оказываются решения, соответствующие первым двум-трем собственным формам колебаний, а это означает, что достаточно решения двух-трех уравнений типа (147), когда i = 1,2,3.
При периодичности внешних возмущающих моментов правые части дифференциальных уравнений также будут периодическими функциями. Для дальнейшего решения обычно производят разложение каждого из возмущающих моментов в ряд Фурье, после этого анализируется влияние каждой гармоники, а затем выполняется сложение всех найденных результатов.
Хотя все эти выкладки выполняются достаточно просто,
они должны быть повторены для всех важнейших гармонических составляющих
возмущения, а число таких гармоник
достаточно велико. Следующий пример (табл. 6) дает представление об
относительной важности различных гармоник возмущения в частном случае одного
четырехтактного двигателя внутреннего сгорания. Как видно, амплитуды гармоник
убывают очень медленно, и в данном случае необходимо учесть в расчете не менее 13-15
гармоник. Еще раз подчеркнем, что разложение возмущающих моментов в ряд Фурье
необязательно, если решение находится при помощи уравнения (147).
Таблица 6
|
Номер составляющей |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Амплитуда составляющей |
2,38 |
2,69 |
2,65 |
2,31 |
1,95 |
1,64 |
1,01 |
0,76 |
0,59 |
0,47 |
Ввиду того,
что угловая скорость вращения может изменяться в процессе эксплуатации, частоты
возмущения ![]() непостоянны; вместе с
изменением режима вращения изменяются и частоты возмущения. При этом становится
реальной возможность совпадения частоты какой-либо гармоники возмущения с одной
из собственных частот. В случае такого совпадения система оказывается в
резонансном режиме и в расчет амплитуд колебаний следует ввести силы неупругого
сопротивления.
непостоянны; вместе с
изменением режима вращения изменяются и частоты возмущения. При этом становится
реальной возможность совпадения частоты какой-либо гармоники возмущения с одной
из собственных частот. В случае такого совпадения система оказывается в
резонансном режиме и в расчет амплитуд колебаний следует ввести силы неупругого
сопротивления.
Полное решение такой задачи даже в простейшем предположении вязких сил трения оказывается очень громоздким, поэтому практические расчеты производят приближенными способами. Основное упрощение состоит обычно в том, что форма колебаний при резонансе принимается совпадающей с соответствующей собственной формой, определенной без учета сил затухания.
Пусть,
например, одна из гармоник возмущающей силы имеет частоту ![]() , равную i-й
собственной частоте
, равную i-й
собственной частоте ![]() . Тогда в расчете колебаний учитывается только i-я собственная форма, и если
имеет место вязкое трение, то вместо уравнения (147) получим
. Тогда в расчете колебаний учитывается только i-я собственная форма, и если
имеет место вязкое трение, то вместо уравнения (147) получим
![]()
где ![]() - коэффициент затухания, зависящий от номера резонирующей
гармоники;
- коэффициент затухания, зависящий от номера резонирующей
гармоники; ![]() - приведенная амплитуда возмущающей силы.
- приведенная амплитуда возмущающей силы.
Это уравнение по смыслу совпадает с уравнением (106). Согласно (110), резонансная амплитуда в данном случае,
![]()
После
вычисления резонансного значения ![]() следует образовать резонансные
значения амплитуд углов поворота. При помощи формул (145) получим, опуская в
каждой строке как малые все слагаемые, кроме i-го:
следует образовать резонансные
значения амплитуд углов поворота. При помощи формул (145) получим, опуская в
каждой строке как малые все слагаемые, кроме i-го:
![]()
3.7. Примеры
расчетов
Пример 17. Два двигателя массой m = 500 кг каждый установлены
на двух балках двутаврового сечения №24 (рис.53,а). При работе левый двигатель
создает возмущающую силу ![]() . Найти амплитуды колебаний двигателей и максимальное
напряжение в балках без учета массы балок. Дано: a = 2 м; F = 1кн; n = 480 об/мин;
. Найти амплитуды колебаний двигателей и максимальное
напряжение в балках без учета массы балок. Дано: a = 2 м; F = 1кн; n = 480 об/мин; ![]() кПа.
кПа.
Решение
Уравнение движения масс:
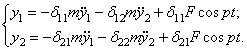
Решение уравнений ищем в виде
![]()
После подстановки получим систему алгебраических уравнений
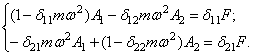
Единичные
эпюры моментов, необходимые для вычисления коэффициентов ![]() представлены на
рис.53,б,в.
представлены на
рис.53,б,в.
Перемножая соответствующие эпюры по способу Верещагина, получим значения перемещений
![]()
![]()
Частота вибрационной нагрузки:
![]()
После подстановки в систему алгебраических уравнений находим амплитуды колебаний:
![]()
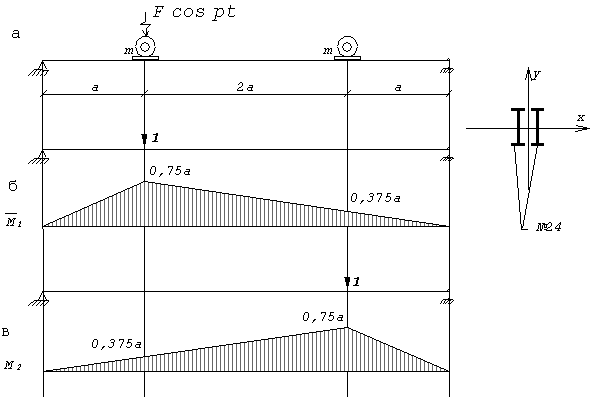
Рис. 53
Соответствующие
динамические нагрузки ![]() и Fg2 определяем из системы
уравнений
и Fg2 определяем из системы
уравнений
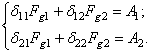
Так как А1 и
А2 близки по величине,
то ![]() м, тогда
м, тогда ![]() кн.
кн.
С учетом статической нагрузки находим
![]() кн.
кн.
Максимальное напряжение в балках:
![]() .
.
Пример 18. Построить эпюру динамических
изгибающих моментов для невесомой балки пролетом l = 4м при действии возмущающей силы ![]() (рис.54,а), если
(рис.54,а), если ![]()
![]()
Решение.
Опуская вид единичных
эпюр(см. пример 7), приведем значения перемещений ![]() :
:
![]()
![]()
![]()
Эпюра от амплитудного значения возмущающей силы показана на рис.54,б.
Перемножая
эпюру ![]() с эпюрами
с эпюрами ![]() и
и ![]() (рис.29) находим:
(рис.29) находим:
![]()
![]()
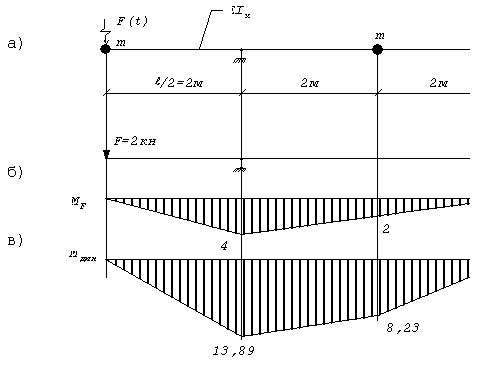
Рис. 54
Собственные частоты колебаний балки вычислены ранее (пример 7) и равны:
![]()
«Исправленные» главные перемещения:
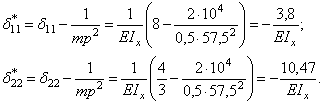
Система канонических уравнений динамического варианта метода сил для вычисления сил инерции X1 и X2 имеет вид:
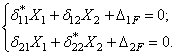
После подстановки числовых значений коэффициентов получим:
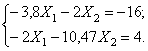
Силы инерции:
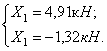
Используя формулу:
![]()
строим эпюру динамических изгибающих моментов Mдин (рис.54,в).
Пример 19. Построить эпюру динамических
изгибающих моментов в симметричной раме (рис.55,а) при действии на нее
симметричной динамической нагрузки ![]() и
и ![]() Частота возмущающих
сил
Частота возмущающих
сил ![]() Сосредоточенные массы
одинаковы и располагаются посредине каждого стержня.
Сосредоточенные массы
одинаковы и располагаются посредине каждого стержня.
Решение.
Так как
вибрационная нагрузка симметрична, то формы вынужденных колебаний также будут
симметричными. Групповые симметричные неизвестные силы инерции показаны на
рис.55,б. Эпюры моментов от единичных сил ![]() и
и ![]() , действующих по направлению сил инерции, показаны на
рис.55,в,г,д. Для их построения можно было применить метод расчета рам,
например, метод сил или метод перемещений. Перемещения
, действующих по направлению сил инерции, показаны на
рис.55,в,г,д. Для их построения можно было применить метод расчета рам,
например, метод сил или метод перемещений. Перемещения ![]() и
и ![]() определяются путем
перемножения этих эпюр. Однако проще перемножать эпюры
определяются путем
перемножения этих эпюр. Однако проще перемножать эпюры ![]() не друг с другом, а с
эпюрами
не друг с другом, а с
эпюрами ![]() , построенными для основных систем и показанными на
рис.55,е,ж,з (основная система на рис.55,е,ж получается путем введения
шарниров, а на рис.55,з - путем разрезания стоек в их средних по высоте
сечениях).
, построенными для основных систем и показанными на
рис.55,е,ж,з (основная система на рис.55,е,ж получается путем введения
шарниров, а на рис.55,з - путем разрезания стоек в их средних по высоте
сечениях).
а)
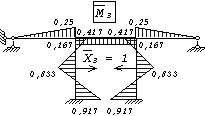
б)
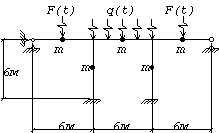
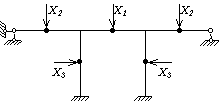
в) г)


д)
е)

ж)
з)
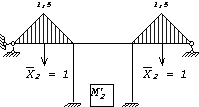

и)
к)
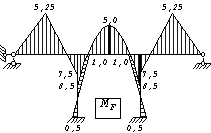
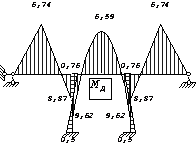
Рис. 55
Опуская промежуточные вычисления, приведем значения перемещений
![]()
Частотный определитель имеет вид:
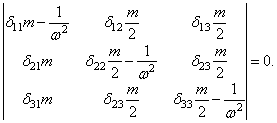
Раскрывая определитель и решая кубическое частотное уравнение, найдем собственные частоты колебаний рамы:
![]()
![]()
![]()
Построив для
заданной системы эпюру MF
от амплитудных значений вибрационных нагрузок (рис.55,и) и перемножив
эту эпюру с вспомогательными эпюрами ![]() , получим перемещения от амплитуд динамических нагрузок:
, получим перемещения от амплитуд динамических нагрузок:
![]()
Частота возмущающих нагрузок:
Главные перемещения с учетом зависимости инерционных сил от частоты p:
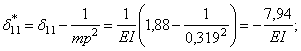
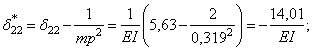
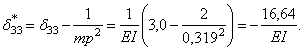
Канонические уравнения динамического варианта метода сил:
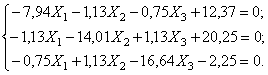
Амплитудные значения сил инерции масс:
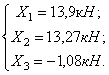
Для построения эпюры динамических изгибающих моментов Mдин (рис. 55, к) вычисляем моменты в характерных сечениях рамы по формуле:
![]()
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Сопротивление материалов
Прикладная механика Строительная механика Теория машин и механизмов