Главная
Раздел 2. Свободные колебания
2.1. Общие сведения о свободных колебаниях
Прежде чем перейти к строгому математическому описанию поведения различных систем при свободных колебаниях, остановимся подробно на природе их возникновения.
Известно, что в ряде случаев тело, получившее некоторое начальное возмущение, после удаления причины этого возмущения продолжает совершать колебания. Эти свободные колебания играют важнейшую роль не только в плане проверки системы на резонанс, т.е. на выявление совпадения одной из собственных частот колебаний с частотой действующих на систему постоянно вибрационных нагрузок. Дело в том, что поведение системы при свободных колебаниях характеризует её "динамическую индивидуальность", которая определяет поведение системы при всех других условиях.
Рассмотрим некоторые примеры возникновения свободных колебаний. После того как по струне рояля ударяет один из молоточков, струна некоторое время продолжает самостоятельно совершать колебания - свободные колебания. Это становится возможным, во-первых, потому, что струна имеет массу и при движении накапливает кинетическую энергию, а во-вторых, потому, что при отклонении от положения равновесия струна накапливает потенциальную энергию .
Точно так же обычный маятник может совершать колебания благодаря тому, что, во-первых, его гиря обладает массой и, во-вторых, при подъёме гири относительно своего низшего положения она накапливает потенциальную энергию.
Аналогично приведенным примерам корабли, летательные аппараты, здания, машины, люди и вообще все тела могут накапливать энергию за счёт изменения формы. Так как все тела обладают ещё и массой, то после тех или иных начальных толчков они могут совершать свободные колебания.
Идеальным объектом исследования свободных колебаний может служить подвешенная за один конец велосипедная цепь. Пусть свободно висящая цепь первоначально находится в состоянии покоя. Свободные колебания можно вызвать, если отклонить цепь каким-либо образом, а затем отпустить или резко её ударить (но так, чтобы боковое перемещение любой точки цепи было малым по сравнению с длиной цепи). При этом можно наблюдать следующее:
1. Развитие движения во времени зависит от того, как оно началось.
2. Движение постепенно затухает.
3. При своем движении цепь не имеет какой-либо определённой формы; с течением времени форма цепи изменяется, однако в конце движения колебания часто характеризуются более или менее отчетливой формой.
4. Невозможно указать "частоту" колебаний, но с течением времени движение может принять определённую частоту.
Кажущийся хаотический характер колебаний можно упорядочить, если надлежащим образом задать начальные условия движения. В этом случае удаётся получить колебания цепи с неизменной формой и определённой частотой. Проще всего этого можно добиться следующим образом. Подвесим цепь к кулисному механизму (рис. 9).
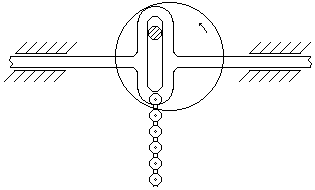
Рис. 9
При вращении кривошипа точка подвеса перемещается в горизонтальном направлении по синусоидальному (т.е. гармоническому) закону. Если при этом регулировать скорость двигателя, приводящего механизм в движение, то можно изменять частоту колебаний точки подвеса. При очень низких частотах цепь будет просто перемещаться из стороны в сторону, сохраняя более или менее вертикальное положение. Однако при возрастании частоты наступает момент, когда цепь начинает интенсивно раскачиваться с частотой, равной частоте возбуждения (рис. 10,а). Эти колебания не являются свободными, так как цепь находится под действием вибрационной нагрузки. Но если внезапно остановить двигатель, т.е. удалить внешнюю нагрузку, то последующие колебания будут свободными и при этом совершенно не такими, как при случайно заданных начальных условиях. Эти колебания будут затухать, но всё время будут сохраняться форма и частота колебаний цепи. Иначе говоря, характер движения с течением времени остаётся неизменным. Можно показать, что существует целый ряд частот начального возбуждения, для каждой из которых характер движения будет иным, но также неизменным во времени. Так, при постепенном увеличении частоты колебаний механизма можно возбудить колебания, во время которых цепь принимает форму, показанную на рис. 10,б.
После резкой остановки точки подвеса такие колебания постепенно затухают, сохраняя при этом свою частоту и форму. При еще более высоких частотах можно получить другие формы колебаний (рис. 10,в,г).
Таким образом, цепь обладает рядом форм свободных колебаний, которые называются собственными формами. Каждой собственной форме соответствуют определённая частота и скорость затухания колебаний.
Собственные частоты системы (разумеется, любой системы, а не только подвешенной цепи), её собственные формы и скорости затухания являются индивидуальными характеристиками системы; они не связаны ни с какими внешними воздействиями.
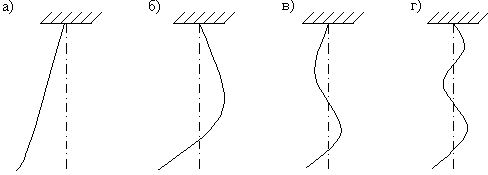
Рис. 10
Экспериментальные исследования показывают, что увеличение массы системы приводит к снижению, а увеличение жёсткости - к возрастанию всех её собственных частот. При этом различные частоты изменяются в разной степени.
Собственные формы колебаний системы обладают следующими свойствами: любая возможная конфигурация системы может быть представлена в виде суперпозиции (наложения) некоторого числа таких конфигураций, каждая из которых соответствует одной собственной форме колебаний. Таким образом, если задать системе некоторую статическую деформацию, а затем освободить систему, то возникнут свободные колебания по всем соответствующим формам; каждое из таких колебаний будет происходить с соответствующей собственной частотой независимо от остальных движений. Любая комбинация двух собственных форм колебаний также является собственной формой.
Теперь перейдём к рассмотрению такой особенности свободных колебаний, как их затухание.
Эффект затухания колебаний объясняется наличием трения; иногда его называют демпфированием. Звук колокола слышен в течение длительного времени после удара, так как нет значительных сил трения, которые привели бы к рассеянию механической энергии за счёт её перехода в тепловую энергию, а рассеяние энергии за счёт излучения звуковых волн происходит весьма медленно. С другой стороны, если раскачать кузов автомобиля, а затем отпустить его, то колебания быстро затухнут. Это объясняется действием специально установленных демпферов.
Рассеяние энергии имеет место в любой колебательной системе. Известно, например, что при вибрациях самолёта часть энергии рассеивается в панелях обшивки за счёт трения в заклёпочных соединениях. Значительным демпфированием должны обладать конструкции зданий, что очень важно с точки зрения поведения здания при землетрясении.
Иногда, если это особенно желательно, можно искусственно вводить трение; так, например, на автомобилях устанавливают демпферы колебаний. Прибор, стрелка которого безостановочно колеблется около положения, соответствующего истинному показанию, доставляет большое неудобство в работе. Поэтому, чтобы стрелка пришла в это положение достаточно быстро, вводится демпфирирование. Чрезмерно сильное трение является столь же вредным, как и недостаточное трение, поскольку в этом случае стрелка перемещается в положение отсчёта слишком медленно.
Существует много способов искусственного введения
трения в систему. Это может быть осуществлено, например, электрическим
способом, но чаще используются чисто механические методы демпфирования.
Перечислим основные из них.
1. Вязкое трение в жидкости. Простейшим примером является гидравлический демпфер, который состоит из поршня, перемещающегося в цилиндре; трение возникает при перетекании жидкости (часто вместо жидкости используется воздух) в тонком зазоре между поршнем и стенкой цилиндра. В некоторых других устройствах используются лопасти, движущиеся в масле или силиконовой жидкости.
2. Материалы с высоким уровнем рассеяния энергии. При ударе по "колоколу", изготовленному из специального сплава меди и марганца, вместо звона слышится глухой стук. В амортизирующих опорах часто используют резину; это связано с её высокими демпфирующими характеристиками. Лопатки компрессоров иногда изготавливают из волокнистых полимерных материалов, обладающих значительным внутренним трением.
3. Демпфирующие покрытия панелей. Существуют такие материалы, нанесение которых на поверхность металлических панелей приводит к тому, что при ударе по панели вместо характерного для металлов звука слышится глухой стук.
4. Сухое трение, возникающее при взаимном скольжении поверхностей в процессе вибрации. Этот способ используется, например, в некоторых компрессорах газовых турбин, где осуществлено шарнирное крепление лопаток к ротору. Кроме того, сухое трение возникает, когда в некоторые пружины с целью демпфирования вставляются пучки металлической проволоки.
5. Слоистые конструкции. Панели, состоящие из тонких металлических листов, разделённых тонким слоем вязкоупругого материала, обладают хорошими звукоизолирующими свойствами.
6. Пенопластовые или резиновые прокладки. Например, электрические лампочки, упакованные в такие прокладки, можно без всякого риска бросать с большой высоты на твёрдый пол.
Таким образом, существуют два вида демпфирования:
искусственно вводимое и связанное с естественными силами трения. Если
искусственно вводимое трение чаще всего допускает теоретическую оценку, то
естественное трение, как правило, не поддается расчёту и должно определяться
экспериментально.
Появление трения или его увеличение не приводит к заметным изменениям частоты и формы собственных колебаний. Поэтому исследование свободных колебаний вначале удобно проводить без учёта трения.
2.2. Свободные колебания системы с одной степенью свободы без трения
В большинстве упругих систем при достаточно малых перемещениях сила упругости линейно зависит от перемещения x. Если начало отсчёта смещения x выбрать так, что при x=0: F=0, то для линейной системы F = cx, где с - коэффициент жесткости системы.
Дифференциальное
уравнение движения системы с одной степенью свободы (рис. 11,а) таково:
![]() . (4)
. (4)
Вид дифференциального уравнения не меняется при действии на систему постоянных сил (например, сил тяжести), если смещение тела отсчитывать от положения его статического равновесия.
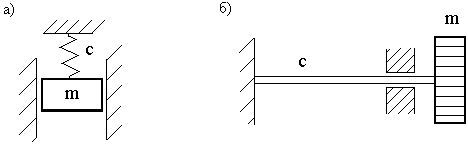
Рис. 11
Действительно, уравнение движения тела массой m (рис.11,а), находящегося под действием силы тяжести и совершающего свободные колебания, имеет вид
![]() , (5)
, (5)
где ![]() - удлинение пружины от силы
тяжести груза.
- удлинение пружины от силы
тяжести груза.
Следовательно, слагаемые mg и cfст в уравнении (5) взаимно уничтожаются, и уравнение (5) совпадает с (4).
Уравнение движения одномассовой системы, совершающей крутильные свободные колебания (рис. 11,б), записывается аналогично:
![]() ,
,
где ![]() - угол поворота тела; J- момент инерции массы m относительно продольной оси вала; с - крутильная жесткость упругой связи.
- угол поворота тела; J- момент инерции массы m относительно продольной оси вала; с - крутильная жесткость упругой связи.
Решение уравнения (4) имеет вид
![]() , (6)
, (6)
где ![]() - угловая частота колебаний, или собственная частота; С1
и С2- постоянные интегрирования, определяемые из начальных условий.
- угловая частота колебаний, или собственная частота; С1
и С2- постоянные интегрирования, определяемые из начальных условий.
Обозначая
смещение и скорость в начальный момент времени t0=0 через x0 и ![]() соответственно, после
подстановки в (6) находим
соответственно, после
подстановки в (6) находим
![]() ,
, ![]() .
(7)
.
(7)
Выражение (6) можно записать иначе:
![]() , (8)
, (8)
где 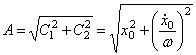 ,
,
![]() .
.
Таким
образом, движение груза при свободных колебаниях одномассовой системы без трения
описывается синусоидальным законом с амплитудой колебаний А, периодом ![]() и начальной фазой
и начальной фазой ![]() (рис.12).
(рис.12).
Период
колебаний ![]() определяется из
условия:
определяется из
условия:
![]() ,
,
откуда
![]() .
(9)
.
(9)
Число колебаний в единицу времени (техническая частота, измеряемая в герцах):
![]() .
(10)
.
(10)
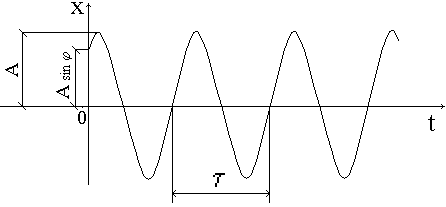
Рис. 12
В практическом
отношении иногда оказывается удобным связать частоту и период колебаний со
статической деформацией fст упругой связи, вызванной силой, равной
весу груза, ![]() .
.
При этом справедливы формулы:
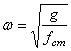 ;
; 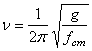 ;
; ![]() . (11)
. (11)
Так как величина fст введена в (11) формально, то очевидна их справедливость независимо от того, совпадает или не совпадает направление силы тяжести с направлением движения груза.
Для анализа свободных колебаний удобно использовать изображение закона движения системы на фазовой плоскости, или так называемый фазовый портрет. Фазовым портретом движения называется графическое изображение зависимости скорости движения от смещения. Для получения фазового портрета продифференцируем выражение (8) по t:
![]() (12)
(12)
Уравнение
движения (8) и выражение (12) представляют собой уравнение фазовой траектории в
параметрической форме. Исключая параметр ![]() , получим
, получим
![]() .
(13)
.
(13)
Уравнение
(13) является уравнением эллипса с полуосями, равными А и ![]() (рис. 13,а). Верхняя
полуплоскость соответствует возрастанию смещения, нижняя - убыванию. Размеры
эллипса зависят от начальных условий, определяющих амплитуду колебаний А.
(рис. 13,а). Верхняя
полуплоскость соответствует возрастанию смещения, нижняя - убыванию. Размеры
эллипса зависят от начальных условий, определяющих амплитуду колебаний А.
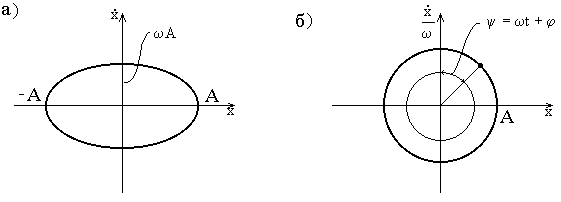
Рис. 13
Все возможные свободные колебания одномассовой системы изображаются семейством эллипсов, каждый из которых соответствует определённому уровню энергии. Чем больше амплитуда колебаний А, тем больше полная энергия системы. Если значения энергии откладывать по оси , перпендикулярной чертежу, то получится поверхность (параболоид), нижняя точка которой соответствует нулевому энергетическому уровню. Точка, изображающая значения смещения и скорости в данный момент времени (изображающая точка), перемещается по горизонтали этой поверхности.
Если изменить
масштаб построения фазовой траектории и откладывать по оси абсцисс х, а по оси
ординат - ![]() , то фазовая траектория (рис. 13,б) будет представлять собой
окружность радиусом А, причём изображающая точка будет равномерно двигаться по
этой окружности с угловой скоростью, равной частоте собственных колебаний
, то фазовая траектория (рис. 13,б) будет представлять собой
окружность радиусом А, причём изображающая точка будет равномерно двигаться по
этой окружности с угловой скоростью, равной частоте собственных колебаний ![]() .
.
При наличии рассеяния энергии изображающая точка перемещается по спирали, приближаясь к началу координат.
2.2.1. Примеры расчётов
Пример 1. К цилиндрической пружине
подвешен груз массой m
= 2 кг = 2 Нс2/м. Груз может перемещаться только в вертикальном
направлении. Определить частоту собственных колебаний груза без учёта и с
учётом массы пружины. Средний диаметр пружины D = 6 см; диаметр проволоки пружины d = 0,6 см; число витков n = 15; плотность материала ![]() ; модуль сдвига G =
; модуль сдвига G =![]() .
.
Решение.
Жесткость пружины:
![]() .
.
Частота собственных колебаний без учёта массы пружины :
![]() .
.
Приведенная
масса пружины:
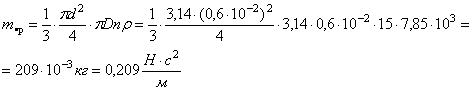
Частота собственных колебаний с учётом массы пружины:
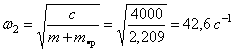 .
.
Пример 2. Определить круговую и
техническую частоту, а также период собственных колебаний сосредоточенного
груза Р = 12 кН, приложенного на свободном конце балки, жестко заделанной
другим концом. Балка представляет собой двутавр № 20 (Jx = 1840 см4)
длиной ![]() = 1 м. Собственным весом балки пренебречь.
= 1 м. Собственным весом балки пренебречь.
Решение.
Статический прогиб балки от веса сосредоточенного груза:
![]() .
.
Частота собственных колебаний:
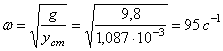 .
.
Период колебаний:
![]() .
.
Техническая
частота:
![]() .
.
Пример 3. К стальному стержню подвешен
груз массой m = 50 кг,
совершающий вертикальные продольные колебания. Длина стержня ![]() = 1 м, диаметр d = 2 см. Определить частоту и период собственных вертикальных
колебаний системы без учёта и с учётом массы стержня.
= 1 м, диаметр d = 2 см. Определить частоту и период собственных вертикальных
колебаний системы без учёта и с учётом массы стержня.
Решение.
Жесткость
стержня:
![]() .
.
Частота
собственных колебаний без учёта массы стержня:
![]() .
.
Соответствующий период колебаний:
![]() .
.
Приведенная масса стержня:
![]() .
.
Собственная частота колебаний с учётом массы стержня:
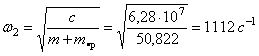 .
.
Соответствующий
период колебаний:
![]() .
.
Пример 4.
Определить
собственную частоту крутильных колебаний двухмассовой системы (рис. 14,а) при
следующих данных: диаметры дисков d1 =0,30 м; d2 = 0,20 м; толщины дисков b1 = 0,02 м; b2 = 0,015 м;
диаметр вала d0
= 0,01 м; длина вала ![]() = 0,8 м.
= 0,8 м.
Рис. 14
Решение.
Дифференциальное уравнение свободных колебаний такой системы имеет вид
![]() ,
,
где ![]() - взаимный угол поворота дисков,
- взаимный угол поворота дисков, 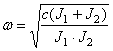 - собственная частота колебаний.
- собственная частота колебаний.
Моменты инерции масс дисков:
![]() ;
;
![]() .
.
Полярный момент инерции поперечного сечения вала:
![]() .
.
Коэффициент жесткости вала при кручении:
![]() .
.
Собственная
частота крутильных колебаний:
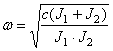 =
=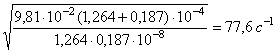 .
.
2.3. Свободные колебания системы с одной степенью свободы при наличии трения
2.3.1 Вязкое трение
В этом случае возникает сопротивление движению, которое пропорционально его скорости. При этом сила сопротивления описывается выражением
![]() , (14)
, (14)
где k- коэффициент пропорциональности.
Примером системы, работающей в условиях вязкого трения, может служить гидравлический амортизатор (рис.15), который создаёт сопротивление движению поршня, зависящее не от перемещения (как это свойственно упругим связям), а от скорости и пропорционально её первой степени (14). Подобные устройства применяются, например, в конструкциях автомобильной подвески. Гидравлический амортизатор состоит из одного или нескольких цилиндров с поршнями или из камеры, в которой может вращаться крыльчатка. Цилиндры и камера наполнены амортизационной жидкостью. При движении поршней или крыльчатки эта жидкость продавливается через калиброванные отверстия; этим создаётся сопротивление, по характеру близкое к вязкому. В формуле (14) R- это сила, действующая на амортизатор, а вязкая реакция амортизатора на колеблющееся тело имеет противоположное направление.
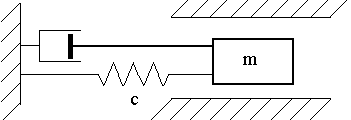
Рис. 15
Дифференциальное уравнение движения в рассматриваемом случае таково:
![]() , (15)
, (15)
или
![]() , (16)
, (16)
где
![]() ;
; ![]() .
.
Для рассматриваемого линейного дифференциального уравнения с постоянными коэффициентами характеристическое уравнение имеет вид
![]() ,
,
![]() .
.
Обозначим
![]() .
.
Тогда решение уравнения (16) определяется формулой
![]() (17)
(17)
или
![]() , (18)
, (18)
где
![]() ;
; ![]() .
.
Следовательно, при наличии вязкого трения движение груза описывается непериодическим законом (рис. 16).
Тем не менее часто это движение называют периодическими затухающими колебаниями, несмотря на очевидную невозможность совмещения понятий "периодические" и "затухающие".
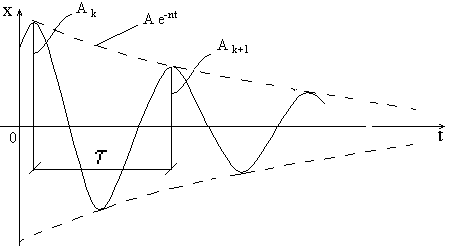
Рис. 16
Под периодом ![]() этих колебаний
понимают время между двумя максимальными смещениями:
этих колебаний
понимают время между двумя максимальными смещениями:
![]() . (19)
. (19)
Величину ![]() называют угловой
частотой затухающих колебаний.
называют угловой
частотой затухающих колебаний.
Отношение двух последовательных максимальных отклонений от положения равновесия
![]() .
(20)
.
(20)
Значит,
последовательные максимальные отклонения системы от равновесного положения
(амплитуды колебаний) представляют собой члены геометрической прогрессии со
знаменателем, равным ![]() .
Чаще рассматривают не отношение двух последовательных амплитуд, а логарифм
этого отношения, который называют логарифмическим
декрементом колебаний:
.
Чаще рассматривают не отношение двух последовательных амплитуд, а логарифм
этого отношения, который называют логарифмическим
декрементом колебаний:
![]() . (21)
. (21)
В металлических конструкциях без специально введенных
элементов трения логарифмический декремент составляет обычно от нескольких
сотых до десятых долей единицы.
Если колебания
затухают медленно и отношение двух последовательных амплитуд ![]() близко к единице, то
близко к единице, то
![]() ,
,
где
![]() ;
;![]() .
.
Таким
образом, при малом затухании логарифмический декремент примерно равен отношению
изменения амплитуды колебаний за период ![]() к амплитуде А.
к амплитуде А.
Так как логарифмический декремент колебаний
![]() ,
,
то
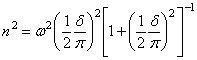 .
.
Подставляя
значение n2 в формулу для ![]() , установим связь между величинами
, установим связь между величинами![]() ,
,![]() и
и ![]() :
:
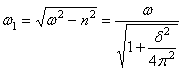 . (22)
. (22)
Из (22)
следует, что даже при значительном затухании частота ![]() затухающих колебаний
мало отличается от частоты
затухающих колебаний
мало отличается от частоты ![]() собственных колебаний
соответствующей системы без трения. Например, при сравнительно большом
затухании, когда каждый следующий размах вдвое меньше предыдущего (
собственных колебаний
соответствующей системы без трения. Например, при сравнительно большом
затухании, когда каждый следующий размах вдвое меньше предыдущего (![]() ), частота
), частота ![]() лишь на 0,6 % меньше,
чем
лишь на 0,6 % меньше,
чем ![]() . Таким образом, можно считать, что трение практически не
влияет на частоту колебаний и
. Таким образом, можно считать, что трение практически не
влияет на частоту колебаний и ![]() .
.
Определим
постоянные интегрирования в решении уравнения затухающих колебаний (17).
Обозначим смещение и скорость в начальный момент времени t0=0 через x0 и ![]() соответственно. После
подстановки в (17) получим
соответственно. После
подстановки в (17) получим
x0=C1; ![]() ,
,
тогда
C1=x0; ![]() ,
,
и решение уравнения (16) , удовлетворяющее начальным условиям, имеет вид
![]() (23)
(23)
Пример 5. Амплитуда собственных колебаний за один период уменьшилась в два раза. Определить логарифмический декремент колебаний и изменение собственной частоты вследствие затухания.
Решение.
Логарифмический декремент колебаний:
![]() ;
;
![]() ,
,
откуда
![]() .
.
Собственная частота колебаний:
![]() ,
,
т. е. изменение собственной частоты вследствие затухания составляет 0,6 %.
2.3.2. Сухое трение
Рассмотрим
движение упруго закрепленного тела массой m по шероховатой поверхности. Как уже отмечалось, в этом случае
говорят, что имеет место сухое трение (рис.17). Сила трения, действующая на
массу m, постоянна по
величине и направлена в сторону, противоположную движению. Уравнение свободных
колебаний такой системы имеет вид
![]() , (24)
, (24)
где знак плюс соответствует этапу движения, на котором скорость положительна, а знак минус - этапу движения, на котором скорость отрицательна.
Зависимость полной действующей на груз силы F=cx![]() R0 от смещения x показана на рис. 18,а.
R0 от смещения x показана на рис. 18,а.
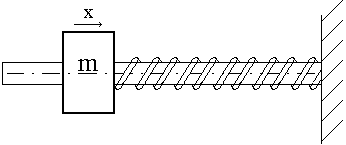
Рис. 17
Перепишем уравнение (24) в виде
![]() . (25)
. (25)
Функция sgn![]() есть единичная
функция, имеющая знак аргумента (рис. 18,б); sgn
есть единичная
функция, имеющая знак аргумента (рис. 18,б); sgn![]() =1 при
=1 при ![]() >0; sgn
>0; sgn![]() =-1 при
=-1 при ![]() <0; sgn=0
при
<0; sgn=0
при ![]() =0.
=0.
Уравнение
(25) содержит нелинейное слагаемое. Тем не менее можно найти решение, если
рассмотреть последовательные интервалы движения, на каждом из которых скорость ![]() имеет
постоянный знак.
имеет
постоянный знак.
Отклоним массу m в крайнее правое положение на величину А и отпустим ее без начальной скорости. В этом случае
x0=A ;![]() .
(26)
.
(26)
Под действием
натяжения пружины на этом этапе груз двигается влево (![]() <0) и уравнение движения
<0) и уравнение движения
![]() ,
,
или
![]() ,
(27)
,
(27)
где
![]() ;
; ![]() .
.
Коэффициент а представляет собой отклонение груза под действием максимально возможной силы трения. При отклонении массы m на величину, меньшую или равную а, движение не начнётся, так как силы упругости пружины недостаточно для преодоления силы трения. Полоса -а<x<a называется зоной застоя. Поэтому уравнение (27) имеет место при А>a.
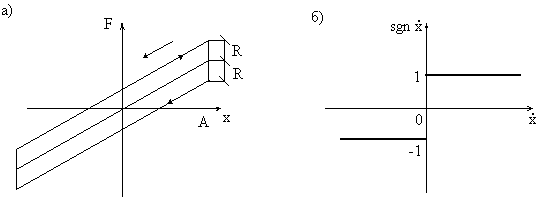
Рис. 18
Общее решение уравнения (27) имеет вид
![]() .
.
Определяя постоянные интегрирования из начальных условий (26) получим
![]() . (28)
. (28)
Закон
движения (28) справедлив до тех пор, пока ![]() <0. Так как
<0. Так как ![]() , то скорость движения будет отрицательной до момента времени
t1,
определяемого из условия:
, то скорость движения будет отрицательной до момента времени
t1,
определяемого из условия: ![]() . В этот момент масса m остановится, смещение x равно
. В этот момент масса m остановится, смещение x равно
![]() ,
,
т. е. под влиянием трения отклонение массы m уменьшилось по абсолютной величине на 2а.
После
остановки масса m начнёт
двигаться вправо. Повторяя приведенные выше расчёты, можно показать, что
движение слева направо также продолжается в течение времени ![]() . Максимальное отклонение вправо равно А-4а. Процесс движения
будет продолжаться до тех пор, пока масса m не остановится в зоне застоя. Зависимость смещения x от времени t на каждом этапе движения
представляет собой косинусоиду, смещённую по оси x на величину а или -а, с амплитудой,
уменьшающейся по закону арифметической прогрессии (рис.18*).
. Максимальное отклонение вправо равно А-4а. Процесс движения
будет продолжаться до тех пор, пока масса m не остановится в зоне застоя. Зависимость смещения x от времени t на каждом этапе движения
представляет собой косинусоиду, смещённую по оси x на величину а или -а, с амплитудой,
уменьшающейся по закону арифметической прогрессии (рис.18*).
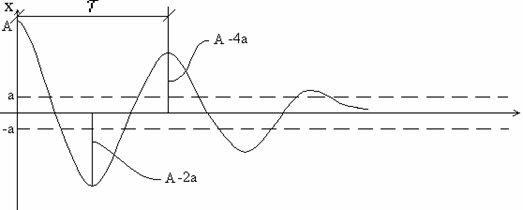
Рис. 18*
Время ![]() между двумя соседними максимумами отклонения, которое условно можно назвать периодом
колебаний,
между двумя соседними максимумами отклонения, которое условно можно назвать периодом
колебаний,
![]() .
.
Наличие сухого трения не меняет частоту колебаний.
Фазовый портрет свободных колебаний системы с сухим трением представлен на рис.19.
В координатах
![]() гармонический закон
движения изображается дугами окружностей.
гармонический закон
движения изображается дугами окружностей.
Если в (27) ввести новую переменную![]() , то получится уравнение гармонических колебаний без трения.
Это движение на фазовой плоскости изображается полуокружностью радиусом
, то получится уравнение гармонических колебаний без трения.
Это движение на фазовой плоскости изображается полуокружностью радиусом ![]() с центром в точке
с центром в точке ![]() . На втором этапе движения, когда
. На втором этапе движения, когда![]() , уравнение движения
, уравнение движения ![]() может рассматриваться
как уравнение гармонических колебаний со смещением
может рассматриваться
как уравнение гармонических колебаний со смещением ![]() . На фазовой плоскости на втором этапе движения получаем
полуокружность с центром в точке
. На фазовой плоскости на втором этапе движения получаем
полуокружность с центром в точке ![]() . И так до тех пор, пока кривая при
. И так до тех пор, пока кривая при ![]() не попадёт в зону
застоя
не попадёт в зону
застоя ![]() .
.
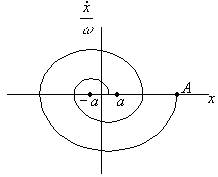
Рис. 19
2.3.3.Позиционное трение
Так
называется вид трения, при котором сила трения пропорциональна смещению.
Рассмотрим систему, состоящую из груза массой m, закреплённого на рессоре, листы
которой собраны без предварительного натяга (рис. 20,а). Сила трения листов
рессоры друг от друга пропорциональна контактному давлению, которое, в свою
очередь, пропорционально смещению![]() . Зависимость между реакцией рессоры, действующей на груз, и
смещением груза
. Зависимость между реакцией рессоры, действующей на груз, и
смещением груза![]() F=¦
F=¦![]() для рассматриваемой системы представлена на рис. 20,б.
для рассматриваемой системы представлена на рис. 20,б.
Обозначим жёсткость системы при увеличении
смещения ![]() по модулю через С
по модулю через С![]() , а жёсткость при уменьшении абсолютного значения смещения -
через С
, а жёсткость при уменьшении абсолютного значения смещения -
через С![]() . Жёсткость упругого элемента системы при отсутствии трения
. Жёсткость упругого элемента системы при отсутствии трения
![]() .
.
а б
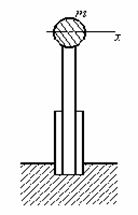
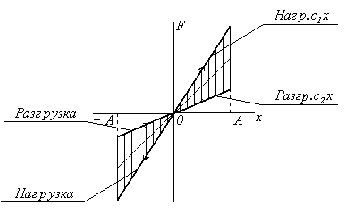
Рис. 20
На каждой
четверти периода характеристика системы прямолинейна, поэтому движение массы m описывается синусоидой. При
переходе через равновесное положение частота собственных колебаний меняется от
![]() до
до ![]() . Отклоним массу m в крайнее правое положение, при этом её скорость в этот момент
. Отклоним массу m в крайнее правое положение, при этом её скорость в этот момент ![]() . Если груз отпустить, то он начнёт двигаться влево под
действием силы упругости, уменьшенной на величину сил трения. Частота
собственных колебаний груза будет
. Если груз отпустить, то он начнёт двигаться влево под
действием силы упругости, уменьшенной на величину сил трения. Частота
собственных колебаний груза будет ![]() , а время движения до равновесного положения -
, а время движения до равновесного положения - ![]() . Скорость груза в равновесном положении станет равной
. Скорость груза в равновесном положении станет равной ![]() . Дальнейшее движение (влево) определяется жёсткостью
. Дальнейшее движение (влево) определяется жёсткостью ![]() , а крайнего левого положения груз достигает через время
, а крайнего левого положения груз достигает через время ![]() . Наибольшее смещение влево равно
. Наибольшее смещение влево равно ![]() .
.
Максимальное отклонение вправо в конце полного периода движения вычисляется по формуле
![]() =
=![]() ,
,
следовательно, логарифмический декремент колебаний:
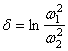 =
=![]() .
.
При малом
затухании, когда разность жесткостей ![]() существенно меньше средней жёсткости
существенно меньше средней жёсткости ![]() , получим
, получим
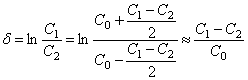 .
.
Характер движения при позиционном трении показан на рис. 21. Из полученных формул следует, что при силе трения, пропорциональной смещению, логарифмический декремент колебаний постоянен и, следовательно, точно так же, как и при вязком трении, последовательные амплитуды составляют геометрическую прогрессию.
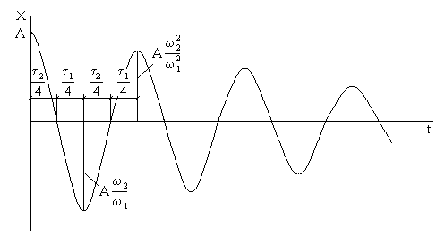
Рис. 21
Как видно из рис. 21, период рассматриваемых затухающих колебаний:
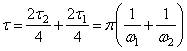 .
.
Соответствующая этому периоду угловая частота:
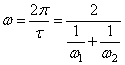 .
.
Частоты ![]() и
и ![]() определяются
выражениями
определяются
выражениями
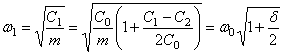 ;
;
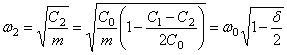 ,
,
где ![]() - собственная частота соответствующей системы без трения.
- собственная частота соответствующей системы без трения.
Тогда
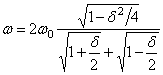 .
.
При небольших
логарифмических декрементах колебаний ![]() это выражение
отличается от собственной частоты колебаний соответствующей системы без трения
на величину второго порядка малости. Поэтому подобно вязкому и сухому трению
позиционное трение практически не влияет на собственную частоту колебаний.
это выражение
отличается от собственной частоты колебаний соответствующей системы без трения
на величину второго порядка малости. Поэтому подобно вязкому и сухому трению
позиционное трение практически не влияет на собственную частоту колебаний.
2.4.Свободные колебания систем с конечным числом степеней свободы (общий случай)
Как уже говорилось (см. подразд. 1.4), дифференциальные уравнения движения таких систем можно получить тремя основными способами: 1) в форме уравнений Лагранжа; 2) прямым способом; 3) обратным способом.
Наиболее общий вид дифференциальных уравнений движения может быть получен в форме уравнений Лагранжа
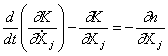 , (29)
, (29)
где K и П -
кинетическая и потенциальная энергии соответственно; ![]() и
и ![]() - обобщённые координаты и обобщённые скорости;
- обобщённые координаты и обобщённые скорости; ![]() число степеней свободы системы.
число степеней свободы системы.
Известно, что при малых колебаниях около положения равновесия кинетическая и потенциальная энергии выражаются через обобщённые координаты и обобщённые скорости следующим образом:
![]() ;
; ![]()
![]() , (30)
, (30)
где ![]() инерционные коэффициенты;
инерционные коэффициенты; ![]() квазиупругие коэффициенты, называемые также обобщёнными
коэффициентами жёсткости.
квазиупругие коэффициенты, называемые также обобщёнными
коэффициентами жёсткости.
Подставляя (30) в (29), получим систему однородных линейных дифференциальных уравнений с постоянными коэффициентами:
![]() ,
, ![]() (31)
(31)
Однако составление уравнений движения по схеме Лагранжа не является обязательным, потому что во многих случаях прямой или обратный способы оказываются более удобными.
Рассмотрим
особенности названных способов на примере системы с двумя степенями свободы,
состоящей из тел с массами ![]() и
и ![]() ,соединённых пружинами с жесткостями
,соединённых пружинами с жесткостями ![]() и
и ![]() (рис. 22,а).
(рис. 22,а).
За обобщённые
координаты примем горизонтальные перемещения ![]() и
и![]() грузов, отсчитываемые от положения равновесия, в которых
отсутствуют деформации пружин. Удлинения пружин в процессе движения:
грузов, отсчитываемые от положения равновесия, в которых
отсутствуют деформации пружин. Удлинения пружин в процессе движения: ![]() ;
; ![]() .
.
Основной способ (уравнения Лагранжа)
Кинетическая энергия рассматриваемой системы:
![]() .
.
Потенциальная энергия деформации пружин:
![]() .
.
Вычислим производные, необходимые для подстановки в уравнения Лагранжа:
![]() ;
; ![]() ;
;
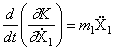 ;
; 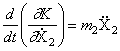 ;
;
![]() ;
; ![]() .
.
Подставляя вычисленные значения в (29), получим дифференциальные уравнения движения рассматриваемой системы
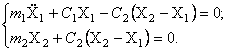 (32)
(32)
Прямой способ
Выделяем массы ![]() и
и
![]() и
рассматриваем их как свободные тела под действием сил упругости, определяемых
удлинениями
и
рассматриваем их как свободные тела под действием сил упругости, определяемых
удлинениями ![]() и
и
![]() обеих
пружин (рис. 22,б):
обеих
пружин (рис. 22,б):
![]()
Дифференциальные уравнения движения грузов имеют вид
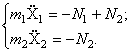
Подставляя
значения ![]() и
и
![]() ,
получим
,
получим
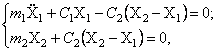
т.е. эти уравнения совпали с уравнениями (32).
а б
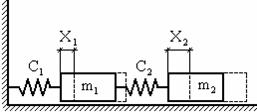
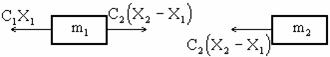
в
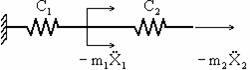
Рис. 22
Обратный способ
Отделяем
грузы и рассматриваем упругий безмассовый скелет системы под действием
кинетических реакций - сил инерции ![]() и
и![]() (рис. 22,в). В этой
схеме первая пружина нагружена силой
(рис. 22,в). В этой
схеме первая пружина нагружена силой ![]() , а вторая - силой
, а вторая - силой ![]() . Перемещение
. Перемещение ![]() конца первой пружины, равное её удлинению, можно записать
в виде
конца первой пружины, равное её удлинению, можно записать
в виде
![]()
Перемещение
правого конца второй пружины ![]() равно сумме удлинений
обеих пружин:
равно сумме удлинений
обеих пружин:
![]()
Из этих
соотношений получим
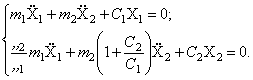
Таким образом, совпали формы записей дифференциальных уравнений движения по основному (уравнения Лагранжа) и прямому способам, а уравнения, полученные обратным способом, отличаются от них по форме. Это связано с тем, что при нашем выборе обобщённых координат кинетическая энергия имеет каноническую форму:
![]() ,
,
т.е. не
содержит произведений скоростей ![]() при
при ![]() . При этом каждое из уравнений Лагранжа содержит только по
одному обобщённому ускорению, как и при использовании прямого способа. Если
обобщённые координаты выбрать так, чтобы потенциальная энергия имела каноническую
форму
. При этом каждое из уравнений Лагранжа содержит только по
одному обобщённому ускорению, как и при использовании прямого способа. Если
обобщённые координаты выбрать так, чтобы потенциальная энергия имела каноническую
форму
![]() ,
,
то уравнения Лагранжа совпали бы с уравнениями, полученными обратным способом.
Сопоставляя полученные
варианты записей по прямому и обратному способам, можно сделать следующее
общее заключение: при составлении системы уравнений по прямому способу ![]() при
при ![]() , а при составлении по обратному способу
, а при составлении по обратному способу ![]() при
при ![]() .
.
Таким образом, пользуясь прямым способом, приходим в общем случае к системе:
![]()
![]() , (33)
, (33)
а применяя обратный способ - к системе:
![]()
![]() . (34)
. (34)
Принципиально
важно, что специальным выбором обобщённых координат можно одновременно придать
каноническую форму как кинетической, так и потенциальной энергии. Такие координаты
![]()
![]() называются нормальными, или главными. При этом
называются нормальными, или главными. При этом
![]() ,
, ![]()
и уравнения Лагранжа принимают вид
![]()
![]() (35)
(35)
Каждое из уравнений (35) интегрируется независимо от других. Иначе говоря, при использовании нормальных координат система представляет собой как бы совокупность независимых парциальных систем с одной степенью свободы.
2.4.1. Решение уравнений движения в общем случае
Частное решение системы уравнений (31) можно записать в виде
![]() ,
, ![]() (36)
(36)
Этими
выражениями описывается моногармонический колебательный режим с частотой ![]() , общей для всех координат
, общей для всех координат ![]() .
.
Подставляя (36) в (31), получим систему алгебраических уравнений:
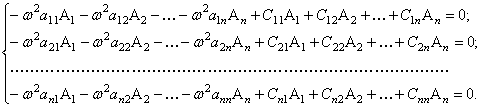 (37)
(37)
Система (37)
является однородной; амплитуды ![]() не могут одновременно равняться нулю, следовательно,
ненулевому решению системы соответствует равенство нулю определителя:
не могут одновременно равняться нулю, следовательно,
ненулевому решению системы соответствует равенство нулю определителя:
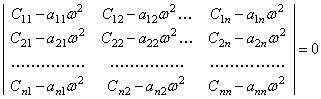 (38)
(38)
Для системы с двумя степенями свободы частотное уравнение оказывается биквадратным:
![]() (39)
(39)
Если положить
здесь ![]() ,
, ![]() , то корни частотного уравнения
, то корни частотного уравнения
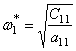 ;
; 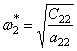
называются парциальными частотами.
Можно
доказать, что парциальные частоты больше меньшей частоты ![]() заданной системы и меньше её большей частоты
заданной системы и меньше её большей частоты ![]() . Отсюда следует, что связь между выбранными обобщёнными координатами,
выраженная параметрами
. Отсюда следует, что связь между выбранными обобщёнными координатами,
выраженная параметрами ![]() и
и ![]() , "раздвигает" значения собственных частот.
, "раздвигает" значения собственных частот.
2.4.2. Решение уравнений движения для простейшей системы
Вернёмся к рассмотрению простейшей системы - с двумя степенями свободы (рис. 22,а), на примере которой проследим получение решения уравнений движения.
Будем искать решение уравнений (32) в виде
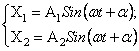 (40)
(40)
Функции (40) не являются общим решением уравнений (32), но позволяют его построить.
Подставляя
(40) в (32), получим
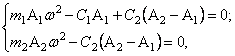
или
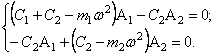 (41)
(41)
Однородная
система (41) имеет тривиальное решение ![]() , которое означает отсутствие колебаний и интереса не
представляет. Ненулевое решение система (41) имеет тогда и только тогда, когда
определитель, составленный из коэффициентов при амплитудах колебаний
, которое означает отсутствие колебаний и интереса не
представляет. Ненулевое решение система (41) имеет тогда и только тогда, когда
определитель, составленный из коэффициентов при амплитудах колебаний ![]() и
и ![]() , равен нулю:
, равен нулю:
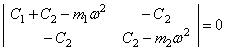 .
.
Этот определитель
называется частотным, а раскрывая его, получим частотное, или
вековое уравнение
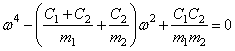 . (42)
. (42)
Это частотное уравнение всегда имеет два вещественных и положительных решения, т.е. система с двумя степенями свободы (рис. 22,а) имеет две собственные частоты:
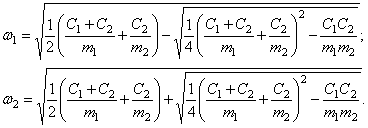 (43)
(43)
Таким
образом, колебательный процесс оказывается двухчастотным и определяется функциями
![]() и
и ![]() . Чтобы отразить в общем решении обе гармоники, усложним
индексацию и запишем решение (40) несколько в ином виде
. Чтобы отразить в общем решении обе гармоники, усложним
индексацию и запишем решение (40) несколько в ином виде
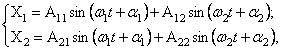 (44)
(44)
где у
амплитуды ![]() индекс i означает номер координаты,
а индекс j - номер
частоты.
индекс i означает номер координаты,
а индекс j - номер
частоты.
Установим
связь между амплитудами ![]() и
и ![]() , используя любое из двух уравнений (41), например, первое:
, используя любое из двух уравнений (41), например, первое:
![]() .
(45)
.
(45)
Подставим в (45)
первую собственную частоту ![]() и перейдём к
двухиндексному обозначению амплитуд (см. выше), тогда получим независящее от
начальных условий отношение амплитуд первой гармоники:
и перейдём к
двухиндексному обозначению амплитуд (см. выше), тогда получим независящее от
начальных условий отношение амплитуд первой гармоники:
![]() . (46)
. (46)
Аналогично из
того же соотношения (45) при ![]() получим для второй
гармоники:
получим для второй
гармоники:
![]() . (47)
. (47)
Следовательно, решение (44) с учётом (46) и (47) можно переписать в виде
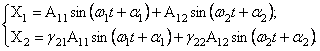 (48)
(48)
В (48)
собственные частоты ![]() и
и ![]() и отношения
и отношения ![]() и
и ![]() зависят только от параметров
колебательной системы. Величины
зависят только от параметров
колебательной системы. Величины ![]() можно определить из
четырёх начальных условий, выражающих значения смещений и скоростей обеих масс
в начальный момент времени.
можно определить из
четырёх начальных условий, выражающих значения смещений и скоростей обеих масс
в начальный момент времени.
Пусть,
например, при ![]() :
:
![]() ;
; ![]() ;
;
![]() ;
; ![]() ,
,
т.е. движение системы вызвано мгновенным ударом по второй массе.
Из (48)
получим
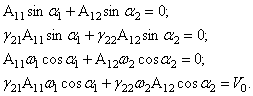
Отсюда
находим
Величины ![]() и
и ![]() можно вычислить по (43),
(46) и (47).
можно вычислить по (43),
(46) и (47).
Искусственным
подбором начальных условий можно добиться одночастотности
колебаний. Например, если сделать так, чтобы ![]() , то колебания будут описываться одной гармоникой:
, то колебания будут описываться одной гармоникой:
![]()
Коэффициент ![]() не зависит от
начальных условий, поэтому рассматриваемые одночастотные колебания
характеризуются вполне определённым, зависящим только от параметров системы,
отношением амплитуд, которое остаётся неизменным в процессе колебаний. Это
отношение определяет первую собственную
форму колебаний.
не зависит от
начальных условий, поэтому рассматриваемые одночастотные колебания
характеризуются вполне определённым, зависящим только от параметров системы,
отношением амплитуд, которое остаётся неизменным в процессе колебаний. Это
отношение определяет первую собственную
форму колебаний.
Если
начальные условия таковы, что ![]() , то колебания будут также одночастотными, но с частотой
, то колебания будут также одночастотными, но с частотой ![]() :
:
![]()
при этом
отношение амплитуд ![]() определяет вторую
собственную форму колебаний.
определяет вторую
собственную форму колебаний.
2.4.3. Ортогональность собственных форм колебаний
При
колебаниях системы по первой собственной форме наибольшие отклонения равны ![]() и
и ![]() ; этим отклонениям соответствуют силы инерции
; этим отклонениям соответствуют силы инерции ![]() и
и ![]() . Аналогично при колебаниях по второй собственной форме
наибольшие отклонения составляют
. Аналогично при колебаниях по второй собственной форме
наибольшие отклонения составляют ![]() и
и ![]() и соответствующие силы
инерции равны
и соответствующие силы
инерции равны ![]() и
и ![]() .
.
Применим к
этим двум состояниям теорему Бетти о взаимности виртуальных работ. Согласно
этой теореме, работа сил первого состояния ![]() на перемещениях
второго состояния
на перемещениях
второго состояния ![]() равна работе сил второго
состояния
равна работе сил второго
состояния ![]() на перемещениях
первого состояния
на перемещениях
первого состояния ![]() , т.е.
, т.е.
![]() ,
,
или
![]() .
.
Так как ![]() , то должно выполняться равенство:
, то должно выполняться равенство:
![]() .
.
Это равенство
выражает свойство ортогональности
двух собственных форм колебаний. После деления на ![]() условие ортогональности можно также записать в виде
условие ортогональности можно также записать в виде
![]() .
.
Если известно
отношение ![]() , определяющее первую собственную форму, то из условия ортогональности
можно найти отношение
, определяющее первую собственную форму, то из условия ортогональности
можно найти отношение ![]() , соответствующее второй собственной форме:
, соответствующее второй собственной форме:
![]() .
.
Обобщая всё сказанное выше, можно отметить, что для любой системы с n степенями свободы выполняется условие ортогональности любых двух собственных форм.
2.4.4. Кратные и нулевые корни частного уравнения
В некоторых случаях могут встречаться кратные корни частного уравнения, а в других случаях среди корней этого уравнения могут оказаться и нулевые.
Рассмотрим эти случаи на примере системы с двумя степенями свободы.
Из соответствующего такой системе частотного уравнения (39) следует, что при выполнении равенства
![]() (49)
(49)
два корня частотного уравнения будут равны друг другу, а при выполнении равенства
![]() (50)
(50)
один из корней частотного уравнения обращается в нуль.
В качестве примера рассмотрим свободные колебания плоской системы с двумя степенями свободы (рис.23).
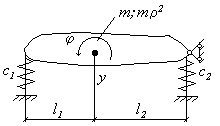
Рис. 23
Обозначим
через ![]() и
и ![]() коэффициенты жёсткости пружин, а через m и
коэффициенты жёсткости пружин, а через m и ![]() - массу и радиус инерции
тела относительно оси, проходящей перпендикулярно плоскости чертежа через центр
тяжести тела. За обобщённые координаты примем вертикальное перемещение центра
тяжести и угол поворота тела
- массу и радиус инерции
тела относительно оси, проходящей перпендикулярно плоскости чертежа через центр
тяжести тела. За обобщённые координаты примем вертикальное перемещение центра
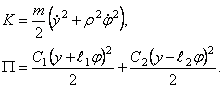
тяжести и угол поворота тела ![]() . Тогда кинетическая и потенциальная энергии имеют вид
. Тогда кинетическая и потенциальная энергии имеют вид
После вычисления соответствующих производных уравнения Лагранжа записываются так:
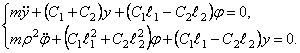
Предположим, что параметры рассматриваемой системы удовлетворяют двум простым (и практически реально осуществимым) соотношениям:
![]() ;
; ![]() ,
,
тогда полученные дифференциальные уравнения принимают более простую форму
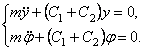 (51)
(51)
Следовательно, инерционные коэффициенты и обобщённые коэффициенты жёсткости в этих уравнениях
![]()
![]()
и условие (49) выполняется, значит, рассматриваемая система имеет две одинаковые собственные частоты колебаний. Для выяснения этого можно было и не привлекать условие (49), так как из уравнений (51) непосредственно следует
![]() .
.
Вследствие независимости уравнений (51) постоянные интегрирования одного уравнения не связаны с постоянными интегрирования другого уравнения
![]()
Для
определения постоянных ![]() служат четыре
начальных условия.
служат четыре
начальных условия.
Рассмотрим пример системы с одной нулевой собственной частотой (рис.24).
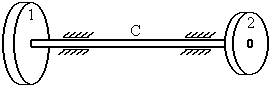
Рис. 24
Обозначим
жёсткость вала на кручение через С;
моменты инерции дисков относительно продольной оси системы - через ![]() и
и ![]() .
.
В качестве
обобщённых координат принимаем углы поворотов дисков ![]() и
и
![]() относительно
некоторого начального положения, в котором вал не закручен.
относительно
некоторого начального положения, в котором вал не закручен.
Кинетическая
и потенциальная энергии системы

После вычисления производных уравнения Лагранжа принимают вид
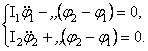 (52)
(52)
Следовательно,
![]()
При этом выполняется
условие (50) и один из корней частотного уравнения равен нулю. Действительно,
подставляя значения коэффициентов в частотное уравнение (39), получим
![]() ,
,
отсюда
![]() ,
, 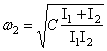 .
.
Выясним физический смысл нулевой частоты. Особенность дифференциальных уравнений (52) состоит в том, что они допускают не только частное решение колебательного типа
![]() (53)
(53)
но также частное решение вида
![]() ,
,
которое описывает равномерное вращение всей системы как жёсткого целого (без закручивания вала). Этому частному решению и соответствует нулевой корень частотного уравнения.
Частному
решению (53) соответствует отличная от нуля частота ![]() ,
а также определённое соотношение амплитуд колебаний
,
а также определённое соотношение амплитуд колебаний
![]() .
.
Таким образом, общее решение уравнений (52) представляется в виде
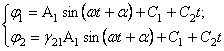 (54)
(54)
и содержит
четыре постоянных интегрирования ![]() , определяемых из начальных условий.
, определяемых из начальных условий.
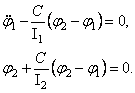
Движение, описываемое законом (54), можно рассматривать как колебания, наложенные на режим равномерного вращения. Чисто колебательную составляющую движения легко выделить путём введения новой переменной (обобщённой координаты)
![]() ,
,
которая представляет собой взаимный угол поворота дисков. Тогда уравнения (52) можно переписать так:
Вычитая
первое уравнение из второго и обозначая ![]() , получим одно дифференциальное уравнение
, получим одно дифференциальное уравнение
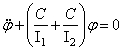 .
.
При этом колебания следуют одночастотному закону
![]() .
.
Можно сказать, что рассматриваемая система имеет только одну колебательную степень свободы; второй степени свободы соответствует вращение системы как жёсткого тела. Аналогично для любой системы с n степенями свободы, когда с валом связаны n дисков, число колебательных степеней свободы на единицу меньше и равно n-1.
2.4.5. Влияние трения на свободные колебания системы с n степенями свободы
Дифференциальные уравнения движения изменятся, если учесть, что при колебаниях возникают силы трения. Рассмотрим случай, когда силы трения линейно зависят от скоростей точек системы (вязкое трение).
Дифференциальные
уравнения (31) в этом случае принимают вид
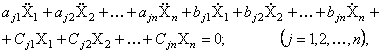 (55)
(55)
или в матричной форме
![]() ,
,
где
 - (56)
- (56)
матрица демпфирования.
Решение уравнений (55) будем искать в виде
![]()
![]() . (57)
. (57)
После
подстановки (57) в (55) получим однородную систему алгебраических уравнений
относительно амплитуд колебаний ![]() , которая в матричной форме выглядит так:
, которая в матричной форме выглядит так:
![]() .
(58)
.
(58)
Ненулевое решение системы (58) возможно тогда и только тогда, когда её определитель равен нулю, что приводит к частотному уравнению
![]() .
(59)
.
(59)
Если все
элементы матрицы демпфирования (56) неотрицательные, то вещественные части всех
корней характеристического уравнения - отрицательные. При этом среди корней
уравнения (59) могут оказаться отрицательные вещественные корни, каждому из
которых, согласно (57), соответствует монотонное затухающее движение
неколебательного характера. Наряду с этим, среди корней могут оказаться и
комплексные сопряжённые корни вида ![]() ;
; ![]()
![]() . Им соответствует затухающее колебательное движение, описываемое
выражением
. Им соответствует затухающее колебательное движение, описываемое
выражением
![]() .
.
Общее решение задачи получится как результат наложения всех частных решений.
2.4.6. Свободные колебания стержневых систем
С изгибными свободными колебаниями многомассовых стержневых систем часто приходится сталкиваться в строительных конструкциях, а также в турбинах, где применяют валы с прямолинейной осью, несущие ряд дисков.
В качестве
примера такой системы рассмотрим шарнирную балку с тремя сосредоточенными
массами ![]() (рис. 25,а).
(рис. 25,а).
Для таких
систем при составлении уравнений движения удобнее использовать обратный способ,
основанный, как уже говорилось, на введении сил инерции, приложенных к
безмассовому упругому "скелету" системы. При этом удобно использовать
понятие единичного перемещения ![]() как перемещения в
направлении i,
вызванного безразмерной единичной силой, действующей в направлении k (рис. 25,б).
как перемещения в
направлении i,
вызванного безразмерной единичной силой, действующей в направлении k (рис. 25,б).
Если на
систему по k-му
направлению действует сила ![]() и требуется определить вызванное ею полное перемещение в i-м направлении, то
вследствие пропорциональности между силой и перемещением (справедлив закон
Гука) можно записать, что
и требуется определить вызванное ею полное перемещение в i-м направлении, то
вследствие пропорциональности между силой и перемещением (справедлив закон
Гука) можно записать, что ![]() . При одновременном действии сил
. При одновременном действии сил ![]() полное перемещение по i-му направлению определяется
суммированием
полное перемещение по i-му направлению определяется
суммированием
![]() .
.
а
б
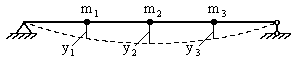
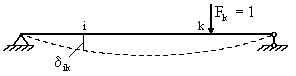
Рис. 25
Итак,
рассмотрим свободные колебания балки, несущей сосредоточенные массы ![]() (рис. 25,а).
Развиваемые ими силы инерции
(рис. 25,а).
Развиваемые ими силы инерции ![]() являются единственной
нагрузкой на упругий "скелет" системы в процессе колебаний. Можно
составить следующие выражения для перемещений точек приложения сосредоточенных
масс под действием этих сил инерции:
являются единственной
нагрузкой на упругий "скелет" системы в процессе колебаний. Можно
составить следующие выражения для перемещений точек приложения сосредоточенных
масс под действием этих сил инерции:
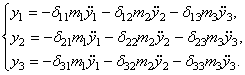 (60)
(60)
Перемещения ![]() вычисляются, как
обычно, методами О. Мора или А.Н. Верещагина от единичных сил, приложенных в местах
действия сил инерции, т.е. в сечениях, где находятся сосредоточенные массы.
вычисляются, как
обычно, методами О. Мора или А.Н. Верещагина от единичных сил, приложенных в местах
действия сил инерции, т.е. в сечениях, где находятся сосредоточенные массы.
Система дифференциальных уравнений (60) имеет частное решение в виде
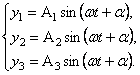 (61)
(61)
Вторые производные этих перемещений по времени, т.е. ускорения, выражаются так:
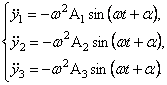 (62)
(62)
Подставляя
(61) и (62) в систему уравнений (60) и сокращая на ![]() , после простейших преобразований получим
, после простейших преобразований получим
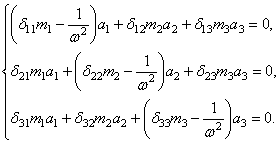 (63)
(63)
Отбрасывая
тривиальное решение этой системы уравнений ![]() как не отвечающее
физическому смыслу рассматриваемой задачи, будем искать ненулевое решение исходя
из условия равенства нулю определителя системы (63):
как не отвечающее
физическому смыслу рассматриваемой задачи, будем искать ненулевое решение исходя
из условия равенства нулю определителя системы (63):
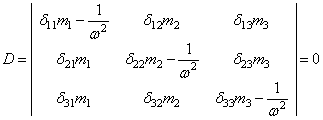 . (64)
. (64)
Частотное
уравнение, получаемое при раскрытии определителя (64) при числе степеней свободы
системы ![]() и
и ![]() , может быть решено строго непосредственно. При
, может быть решено строго непосредственно. При ![]() получение решения
может оказаться затруднительным или даже невозможным.
получение решения
может оказаться затруднительным или даже невозможным.
Если
направления перемещений ![]() выбраны так, что
побочные перемещения
выбраны так, что
побочные перемещения ![]() обращаются в нуль, то
система дифференциальных уравнений (60) и соответствующее ей уравнение частот
распадаются на отдельные уравнения, содержащие только главные перемещения
обращаются в нуль, то
система дифференциальных уравнений (60) и соответствующее ей уравнение частот
распадаются на отдельные уравнения, содержащие только главные перемещения ![]() . В этом случае перемещения
. В этом случае перемещения ![]() называются главными координатами, а соответствующие
формы колебаний - главными формами колебаний.
называются главными координатами, а соответствующие
формы колебаний - главными формами колебаний.
Главные формы колебаний обособлены друг от друга и
каждая из них происходит со своей определённой частотой, которая выражается
формулой, аналогичной формуле для вычисления собственной частоты системы с
одной степенью свободы
![]() .
.
Выбор главных
координат для систем с числом степеней свободы, большим двух, в общем случае
весьма затруднителен. При ![]() это возможно всегда.
это возможно всегда.
Для симметричных систем с симметрично расположенными массами возможны прямо симметричные и обратно симметричные формы колебаний, при которых силы инерции будут соответственно прямо симметричны и обратно симметричны. В этом случае перемещения вычисляются как групповые от парных прямо симметричных или обратно симметричных единичных сил. Побочные перемещения, связывающие прямо симметричные и обратно симметричные силы инерции, обращаются в нуль. Это также приводит к распаду частотного уравнения на два независимых уравнения, из которых одно позволяет найти частоты прямо симметричных колебаний, а другое - обратно симметричных. Так как групповые перемещения определяются от парных единичных сил, то соответствующая масса должна входить в частотные уравнения с коэффициентом 0,5.
2.4.7. Крутильные колебания валов
Рассмотрим крутильные колебания многомассовой системы (рис. 26), которая является общепринятой эквивалентной схемой для расчёта крутильных колебаний коленчатых валов. Коленчатый вал приводится к эквивалентной схеме путём следующих замен: момент инерции заменяющего диска относительно оси вала должен быть равен моменту инерции колена относительно той же оси, при этом учитывается присоединённая масса шатуна; жёсткость на кручение участка заменяющего вала должна быть равна жёсткости на кручение соответствующего участка коленчатого вала.
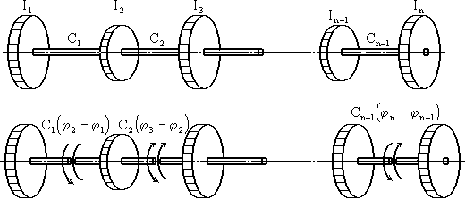
Рис. 26
Эти замены являются неплохой аппроксимацией, хотя и не обеспечивают полной эквивалентности обеих схем. Приведенный момент инерции масс колена и шатуна изменяется в процессе вращения коленчатого вала, поэтому замена колена диском с постоянным моментом инерции не является строгой. Кроме того, при действии на коленчатый вал двух противоположно направленных пар деформация будет заключаться не только в закручивании участка между парами: вследствие изгиба произойдёт закручивание и других участков.
Тем не менее экспериментальные исследования подтверждают приемлемость эквивалентной схемы при достаточно тщательном определении эквивалентных моментов инерции и особенно эквивалентных жёсткостей.
Обозначим
через ![]() моменты инерции масс
дисков относительно продольной оси вала;
моменты инерции масс
дисков относительно продольной оси вала; ![]() - коэффициенты жёсткости участков при кручении;
- коэффициенты жёсткости участков при кручении; ![]() - углы поворотов дисков вокруг продольной оси вала (рис.
26,а).
- углы поворотов дисков вокруг продольной оси вала (рис.
26,а).
Крутильные моменты, действующие в сечениях вала, зависят от взаимного поворота двух смежных дисков и определяются формулами
на первом участке
![]() ;
;
на втором участке
![]() ;
;
![]()
на ![]() - м участке
- м участке
![]()
Уравнения
движения удобнее всего составлять прямым способом (рис. 26,б).
 (65)
(65)
Число этих
уравнений ![]() совпадает с числом дисков, т.е. с числом степеней свободы системы.
совпадает с числом дисков, т.е. с числом степеней свободы системы.
Одним из решений системы (65) является
![]() ,
(66)
,
(66)
описывающее равномерное вращение вала и дисков как жёсткого целого.
Кроме того, возможно решение, описывающее упругие колебания системы
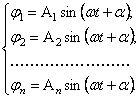 (67)
(67)
Подставляя
(67) в (65), получим
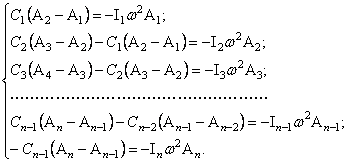 (68)
(68)
Система уравнений
(68) содержит ![]() неизвестных: n амплитуд и частоту
колебаний
неизвестных: n амплитуд и частоту
колебаний ![]() .
.
Если
преобразовать систему (68) и рассматривать её как однородную систему линейных
алгебраических уравнений относительно неизвестных амплитуд ![]() , то ненулевое её решение можно получить, как это
неоднократно делалось выше, из условия равенства нулю определителя. Раскрывая
определитель, получим частотное уравнение.
, то ненулевое её решение можно получить, как это
неоднократно делалось выше, из условия равенства нулю определителя. Раскрывая
определитель, получим частотное уравнение.
Для
иллюстрации сказанного запишем систему (68) в преобразованном виде при ![]()
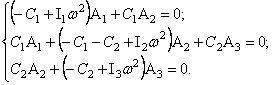
Отсюда получим частотный определитель
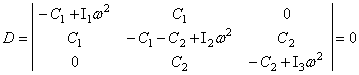 (69)
(69)
и частотное уравнение
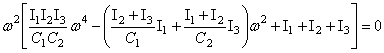 .
(70)
.
(70)
В общем
случае степень частотного уравнения относительно ![]() равна n. Один из корней всегда
равен нулю и соответствует повороту всех дисков и вала как жёсткого целого.
Остальные
равна n. Один из корней всегда
равен нулю и соответствует повороту всех дисков и вала как жёсткого целого.
Остальные ![]() корней (собственных
частот) соответствуют упругим колебаниям.
корней (собственных
частот) соответствуют упругим колебаниям.
При ![]() решение частотного
уравнения представляет значительные трудности. Но цепная структура уравнений
(68) позволяет упростить определение собственных частот при помощи метода
последовательных приближений (метода остатков). Суть метода состоит в следующем.
Принимая
решение частотного
уравнения представляет значительные трудности. Но цепная структура уравнений
(68) позволяет упростить определение собственных частот при помощи метода
последовательных приближений (метода остатков). Суть метода состоит в следующем.
Принимая ![]() и задаваясь ориентировочным значением
и задаваясь ориентировочным значением ![]() , из первого уравнения системы (68) находят амплитуду
, из первого уравнения системы (68) находят амплитуду ![]() ; из второго уравнения системы можно определить амплитуду
; из второго уравнения системы можно определить амплитуду ![]() , из третьего уравнения - амплитуду
, из третьего уравнения - амплитуду ![]() и, наконец, из
предпоследнего уравнения - амплитуду
и, наконец, из
предпоследнего уравнения - амплитуду ![]() . Если в последнее уравнение системы (68) подставить
вычисленные значения
. Если в последнее уравнение системы (68) подставить
вычисленные значения ![]() и
и ![]() , то оно, вообще говоря, не будет удовлетворяться вследствие
произвольности исходного значения
, то оно, вообще говоря, не будет удовлетворяться вследствие
произвольности исходного значения ![]() (которое, по сути,
является первым приближением). Полученное значение левой части (остаток)
характеризует меру неточности первого приближения
(которое, по сути,
является первым приближением). Полученное значение левой части (остаток)
характеризует меру неточности первого приближения ![]() и одновременно
показывает, в какую сторону нужно изменить расчётное значение
и одновременно
показывает, в какую сторону нужно изменить расчётное значение ![]() во втором приближении.
во втором приближении.
Далее
производят повторный расчёт при новом значении ![]() . Знак и величина нового остатка помогут указать необходимую
поправку в значении
. Знак и величина нового остатка помогут указать необходимую
поправку в значении ![]() для следующего
приближения. Расчёт повторяется до тех пор, пока не будет достигнут
удовлетворительный результат в последнем уравнении.
для следующего
приближения. Расчёт повторяется до тех пор, пока не будет достигнут
удовлетворительный результат в последнем уравнении.
При реализации метода удобнее всего использовать компактную табличную схему вычислений, основанную на соотношениях типа
![]() , (71)
, (71)
которые получаются из уравнений (68) после сложения первых i уравнений системы. Соотношение (71) выражает равенство крутящего момента в сечении i-го участка вала (левая часть) сумме моментов сил инерции всех расположенных слева дисков (правая часть).
Задаваясь
значением ![]() и принимая
и принимая ![]() , находим из соотношения (71) для
, находим из соотношения (71) для ![]() :
:
![]() .
.
Далее из того
же соотношения для ![]() :
:
![]() .
.
Общая формула
имеет вид
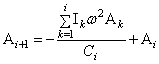 .
.
Процесс
продолжается таким образом до ![]() - го уравнения. После определения из него
- го уравнения. После определения из него ![]() можно переходить к
последнему уравнению и вычислять его левую часть. Этот результат должен быть
равен нулю, так как если сложить все уравнения типа (71), то должно получиться
можно переходить к
последнему уравнению и вычислять его левую часть. Этот результат должен быть
равен нулю, так как если сложить все уравнения типа (71), то должно получиться
![]() .
.
Вследствие неточности принятого исходного
значения ![]() нуля в результате не
получится. Остаток выражает неуравновешенный момент, который при точном выборе
нуля в результате не
получится. Остаток выражает неуравновешенный момент, который при точном выборе
![]() должен быть равен
нулю.
должен быть равен
нулю.
После
нескольких расчётов такого типа (при разных значениях ![]() ) можно построить кривую зависимости остатка R от
) можно построить кривую зависимости остатка R от ![]() (рис.27).
(рис.27).
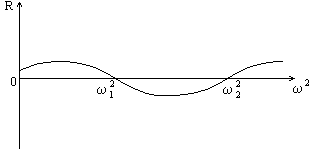
Рис. 27
Точки пересечения кривой с осью абсцисс соответствуют истинным значениям частот.
Объём вычислений может быть значительно уменьшен, если известны ориентировочные значения частот, для определения которых часто используют замену заданной системы упрощённой трехмассовой системой.
При записи решения (67) предполагалось, что колебания являются одночастотными, т.е. для любого диска описываются одной гармоникой
![]() .
.
Существование
спектра частот ![]() требует обобщения
решения (67) и записи его в виде
требует обобщения
решения (67) и записи его в виде
![]()
![]() ,
,
где первый индекс у амплитуды означает номер диска, а второй индекс - номер соответствующей частоты.
Для получения
общего решения необходимо также учесть возможность вращения всей системы как
жёсткого целого (что соответствует частоте ![]() ), т.е. добавить слагаемое вида (66), и тогда общее решение
уравнений движения (65)
), т.е. добавить слагаемое вида (66), и тогда общее решение
уравнений движения (65)
![]()
![]() (72)
(72)
Уравнения
(72) содержат 2n
неизвестных: ![]() неизвестных амплитуд
колебаний первого диска
неизвестных амплитуд
колебаний первого диска ![]() ;
; ![]() неизвестных начальных фаз
неизвестных начальных фаз ![]() ;
угловое смещение
;
угловое смещение ![]() и угловую скорость
и угловую скорость ![]() . Амплитуды колебаний всех остальных дисков
. Амплитуды колебаний всех остальных дисков ![]() определяются через амплитуды составляющих
колебаний первого диска
определяются через амплитуды составляющих
колебаний первого диска ![]() ;
отношения
;
отношения ![]() зависят от номера частоты k и определяют соответствующие формы
колебаний.
зависят от номера частоты k и определяют соответствующие формы
колебаний.
Таким образом, для полного решения задачи необходимо и достаточно указать 2n начальных условий - угловые смещения и угловые скорости всех n дисков.
При произвольно заданных начальных условиях колебания каждого диска будут многочастотными, т.е. будут представлять собой сумму гармоник. Если начальные условия смещения соответствуют одной из собственных форм колебаний, то в дальнейшем процессе будут реализованы эта и только эта собственная форма и соответствующая собственная частота. В общем случае колебания будут носить сложный характер и представлять собой совокупность n форм колебаний. Относительное значение каждого из них зависит от близости заданной системы начальных смещений к той или иной собственной форме.
2.4.8. Примеры расчётов
Пример 6. Пружина несёт две массы ![]() каждая - одна на конце пружины, другая
посередине (рис. 28,а). Средний диаметр пружины
каждая - одна на конце пружины, другая
посередине (рис. 28,а). Средний диаметр пружины ![]() ;
диаметр проволоки пружины
;
диаметр проволоки пружины ![]() ;
число витков на каждой половине пружины
;
число витков на каждой половине пружины ![]() .
Определить частоты собственных колебаний системы.
.
Определить частоты собственных колебаний системы.
а б
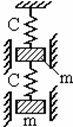
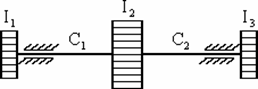
Рис. 28
Решение
Уравнения
движения системы
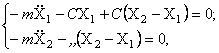
где ![]() и
и ![]() - смещения верхней и нижней масс соответственно; С -
жёсткость пружины.
- смещения верхней и нижней масс соответственно; С -
жёсткость пружины.
Решение системы уравнений ищем в виде
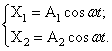
После подстановки получим систему однородных алгебраических уравнений
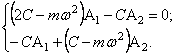
Частотное уравнение
![]() ,
,
или
![]() .
.
Корни частотного уравнения:
![]() ;
; ![]() .
.
Жёсткость
пружины:
Собственные
частоты:
![]() .
.
Пример 7. Определить частоты собственных колебаний невесомой консольной балки с двумя равными сосредоточенными массами (рис. 29,а). Построить собственные формы колебаний, проверить их ортогональность.
Решение
Прикладываем
поочередно силу ![]() в точках расположения
масс m1 и m2 и строим эпюры
изгибающих моментов
в точках расположения
масс m1 и m2 и строим эпюры
изгибающих моментов ![]() (рис. 29,б).
(рис. 29,б).![]()
Путем перемножения соответствующих эпюр способом Верещагина вычисляем единичные перемещения:
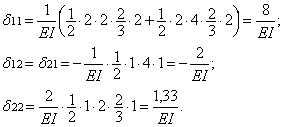
Частотный
определитель:
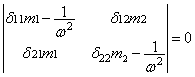 ,
,
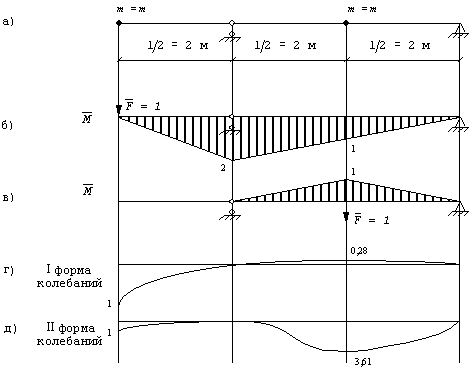
Рис. 29
Или
![]()
где ![]()
Частотное
уравнение:
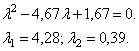
Собственные
частоты колебаний:
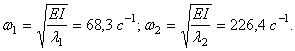
Система алгебраических уравнений относительно амплитуд колебаний А1 и А2:
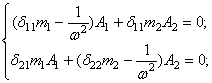
Полагая А1=1,
находим А2 из первого уравнения системы сначала при ![]() , а затем при
, а затем при ![]() :
:
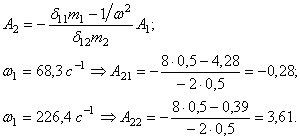
Формы колебаний представлены на рис. 29,г,д.
Проверяем
выполнение условия ортогональности:
![]()
Пример 8. Определитель частоты
свободных колебаний балки с тремя равными сосредоточенными массами m (рис. 30,а), если m=0,5 ![]() ;
; ![]() =8 м;
=8 м; ![]()
Решение
Так как система
и расположенные на ней массы симметричны, то задача может быть решена с
использованием симметрии.
Строим
единичные эпюры изгибающих моментов ![]() (рис. 30,б,в,г).
(рис. 30,б,в,г).
Вычисляем единичные перемещения путем перемножения соответствующих эпюр по способу Верещагина:
.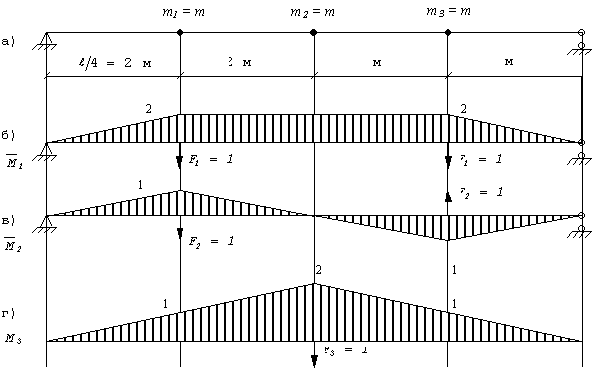
Рис. 30
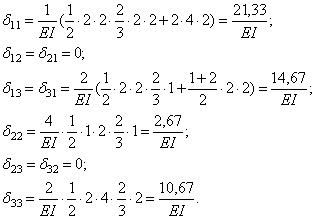
Определитель
для симметричных колебаний составляем с учетом того, что перемещения от
групповой силы ![]() , состоящей из двух сил, получились удвоенными, поэтому
соответствующая масса вводится с коэффициентом 0,5:
, состоящей из двух сил, получились удвоенными, поэтому
соответствующая масса вводится с коэффициентом 0,5:
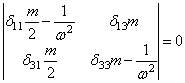 ,
,
или
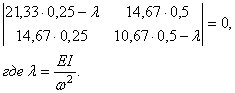
Соответствующее
частотное уравнение:
![]()
Собственные
частоты симметричных колебаний:
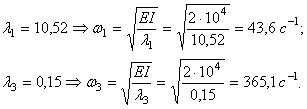
Частотное уравнение для обратно симметричных колебаний:
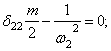
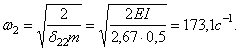
Пример 9. Определить собственные
частоты и формы колебаний системы, состоящей из трех дисков с моментами инерции
масс ![]() укрепленных на стальном валу с жестокостями
укрепленных на стальном валу с жестокостями ![]() (рис. 28,б).
(рис. 28,б).
Решение
Уравнения движения системы, составленные прямым методом, таковы:
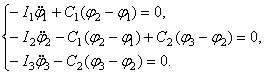
Решение
системы ищем в виде
![]()
После подстановки получаем систему однородных алгебраических уравнений:
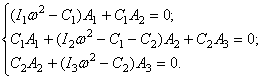
Приравнивая определитель системы нулю и раскрывая его, получим частотное уравнение
![]()
Собственные
частоты колебаний:
![]()
Нулевая частота соответствует повороту вала и дисков как жесткого целого.
Для ненулевых частот определяем собственные формы колебаний, принимая А2 = 1.
Соотношение
между амплитудами:
![]()
Первая форма
колебаний при ![]() :
:
![]()
Вторая форма колебаний
при ![]() :
:
![]()
Пример 10. Методом последовательных приближений определить две низших частоты собственных колебаний судовой дизельной установки по уточненной схеме, состоящей из дисков 1-6, к которым приведены кривошипы двигателей, маховика 7 и гребного винта 8 с присоединенными массами гребного вала и воды (рис.31,а) при следующих данных:
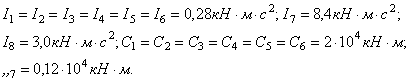
Значения частот в первом приближении определить для упрощенной трехдисковой схемы (рис. 31,б).
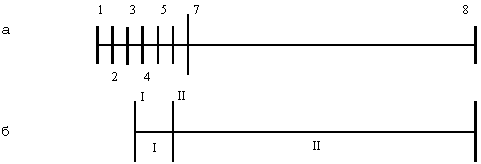
Рис. 31
Решение
Для приближенного определения двух низших частот образуем упрощенную схему (рис.31,б), в которой первые шесть дисков заменены одним общим, причем
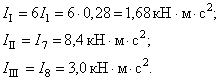
Длина участка
![]() в упрощенной схеме в
3,5 раза больше длины каждого участка между дисками 1-6 в исходной схеме,
поэтому жесткости участков вала в упрощенной схеме
в упрощенной схеме в
3,5 раза больше длины каждого участка между дисками 1-6 в исходной схеме,
поэтому жесткости участков вала в упрощенной схеме
Таблица 1
|
№ диска |
I |
|
A |
|
|
C |
|
|
1 |
0,28 |
144,48 |
1,000 |
144,48 |
144,48 |
2.104 |
0,007 |
|
2 |
0,28 |
144,48 |
0,993 |
143,47 |
287,95 |
2.104 |
0,014 |
|
3 |
0,28 |
144,48 |
0,979 |
141,45 |
429,40 |
2.104 |
0,021 |
|
4 |
0,28 |
144,48 |
0,958 |
138,34 |
567,74 |
2.104 |
0,028 |
|
5 |
0,28 |
144,48 |
0,930 |
134,31 |
702,05 |
2.104 |
0,035 |
|
6 |
0,28 |
144,48 |
0,895 |
129,29 |
831,34 |
2.104 |
0,042 |
|
7 |
8,4 |
4334,4 |
0,853 |
3699,12 |
4530,46 |
1,2.103 |
3,775 |
|
8 |
3,0 |
1548,0 |
-2,922 |
-4523,85 |
6,61 |
|
|
В соответствии с (70) частотное уравнение для упрощенной схемы имеет вид
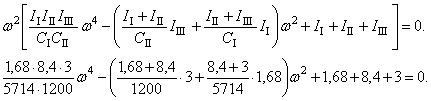
Приближенные значения двух низших частот:
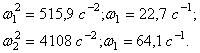
В качестве
первого приближения для уточнения первой собственной частоты колебаний
принимаем ![]() . Результаты расчетов представлены в табл. 1.
. Результаты расчетов представлены в табл. 1.
Полученное
значение остатка ![]() = 6,61 означает, что
принятое в первом приближении значение
= 6,61 означает, что
принятое в первом приближении значение ![]() незначительно
отличается от истинного, поэтому во втором приближении принимаем:
незначительно
отличается от истинного, поэтому во втором приближении принимаем: ![]() . Результаты расчетов сведены в табл. 2.
. Результаты расчетов сведены в табл. 2.
Таблица 2
|
№ диска |
I |
|
A |
|
|
C |
|
|
1 |
0,28 |
148,4 |
1,000 |
148,4 |
148,4 |
2.104 |
0,007 |
|
2 |
0,28 |
148,4 |
0,993 |
147,3 |
295,7 |
2.104 |
0,015 |
|
3 |
0,28 |
148,4 |
0,978 |
145,2 |
440,9 |
2.104 |
0,022 |
|
4 |
0,28 |
148,4 |
0,956 |
141,9 |
582,8 |
2.104 |
0,029 |
|
5 |
0,28 |
148,4 |
0,927 |
137,6 |
720,4 |
2.104 |
0,036 |
|
6 |
0,28 |
148,4 |
0,891 |
132,2 |
852,6 |
2.104 |
0,043 |
|
7 |
8,4 |
4452,0 |
0,848 |
3776,9 |
4629,5 |
1,2.103 |
3,858 |
|
8 |
3,0 |
1590,0 |
-3,01 |
-4785,8 |
-156,3 |
|
|
Остаток ![]() = -156,3 имеет знак,
противоположный полученному в первом приближении. Следовательно, можно
утверждать, что истинное значение величины
= -156,3 имеет знак,
противоположный полученному в первом приближении. Следовательно, можно
утверждать, что истинное значение величины ![]() лежит в пределах (516
лежит в пределах (516![]() 530) с-2.
530) с-2.
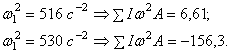
Используя
линейную интерполяцию, находим достаточно точное значение ![]() :
: ![]()
Для уточнения
второй собственной частоты в качестве первого приближения принимаем ![]() Результаты расчетов
представлены в табл. 3.
Результаты расчетов
представлены в табл. 3.
Таблица 3
|
№ диска |
I |
|
A |
|
|
C |
|
|
1 |
0,28 |
1150,2 |
1,000 |
1150,2 |
1150,2 |
2.104 |
0,058 |
|
2 |
0,28 |
1150,2 |
0,943 |
1083,5 |
2233,7 |
2.104 |
0,112 |
|
3 |
0,28 |
1150,2 |
0,830 |
955,0 |
3188,7 |
2.104 |
0,159 |
|
4 |
0,28 |
1150,2 |
0,671 |
771,3 |
3960,0 |
2.104 |
0,198 |
|
5 |
0,28 |
1150,2 |
0,473 |
544,0 |
4505,0 |
2.104 |
0,225 |
|
6 |
0,28 |
1150,2 |
0,248 |
285,0 |
4789,0 |
2.104 |
0,239 |
|
7 |
8,4 |
34507,2 |
0,009 |
295,0 |
5084,0 |
1,2.103 |
4,237 |
|
8 |
3,0 |
12324,0 |
-4,228 |
-52102,0 |
-47018,0 |
|
|
Полученное
значение остатка ![]() = -47018,0 очень
велико, поэтому для второго приближения необходимо значительно изменить
величину
= -47018,0 очень
велико, поэтому для второго приближения необходимо значительно изменить
величину ![]() . Принимаем на втором шаге
. Принимаем на втором шаге ![]() . Результаты расчета сведены в табл. 4.
. Результаты расчета сведены в табл. 4.
Таблица 4
|
№ диска |
I |
|
A |
|
|
C |
|
|
1 |
0,28 |
1400 |
1,000 |
1400 |
1400 |
2.104 |
0,070 |
|
2 |
0,28 |
1400 |
0,930 |
1302 |
2702 |
2.104 |
0,135 |
|
3 |
0,28 |
1400 |
0,795 |
1113 |
3815 |
2.104 |
0,191 |
|
4 |
0,28 |
1400 |
0,604 |
846 |
4661 |
2.104 |
0,233 |
|
5 |
0,28 |
1400 |
0,371 |
519 |
5180 |
2.104 |
0,259 |
|
6 |
0,28 |
1400 |
0,112 |
157 |
5337 |
2.104 |
0,267 |
|
7 |
8,4 |
42000 |
-0,155 |
-6503 |
-1166 |
1,2.103 |
-0,972 |
|
8 |
3,0 |
15000 |
0,817 |
12255 |
11089 |
|
|
Остаток ![]() имеет знак, противоположный полученному в первом
приближении. Следовательно, можно утверждать, что точное значение величины
имеет знак, противоположный полученному в первом
приближении. Следовательно, можно утверждать, что точное значение величины ![]() лежит в интервале
(4108
лежит в интервале
(4108![]() 5000) с-2.
5000) с-2.
Путем линейной интерполяции находим
![]()
Полученное значение
собственной частоты ![]() не является точным,
хотя и близко к нему. Для уточнения значения
не является точным,
хотя и близко к нему. Для уточнения значения ![]() необходимо максимально
сузить интервал, в котором остаток
необходимо максимально
сузить интервал, в котором остаток ![]() меняет знак, что
требует заполнения еще по меньшей мере двух таблиц.
меняет знак, что
требует заполнения еще по меньшей мере двух таблиц.
2.4.9. Свободные колебания автомобиля
Рассмотрим автомобиль как систему упругосвязанных между собой жестких тел (рис. 32,а). Здесь тело 1 схематически представляет собой кузов автомобиля, тела 2-5 - колеса, массы которых будем считать сосредоточенными.
Движение такой системы в процессе колебаний характеризуется семью координатами:
![]() - вертикальное перемещение центра тяжести кузова;
- вертикальное перемещение центра тяжести кузова;
![]() - вертикальные перемещения центров тяжести колес;
- вертикальные перемещения центров тяжести колес;
![]() - угол поворота кузова относительно поперечной оси;
- угол поворота кузова относительно поперечной оси;
![]() - угол поворота кузова относительно продольной оси.
- угол поворота кузова относительно продольной оси.
Распределение
масс автомобиля и жестокостей упругих связей почти симметрично относительно
средней продольной плоскости, поэтому в расчетах колебаний некоторой малой
асимметрией можно пренебречь. При этом общий процесс колебаний можно
рассматривать состоящим из двух взаимно не связанных процессов (рис. 32,б,в): продольных колебаний, характеризуемых
вертикальным перемещением кузова ![]() , поворотом кузова вокруг поперечной оси
, поворотом кузова вокруг поперечной оси ![]() и попарно равными
перемещениями обоих передних колес
и попарно равными
перемещениями обоих передних колес ![]() и обоих задних колес
и обоих задних колес ![]() ; поперечных (боковых)
колебаний, характеризуемых поворотом кузова вокруг продольной оси
; поперечных (боковых)
колебаний, характеризуемых поворотом кузова вокруг продольной оси ![]() и попарно равными
перемещениями обоих левых колес
и попарно равными
перемещениями обоих левых колес ![]() и обоих правых колес
и обоих правых колес ![]()
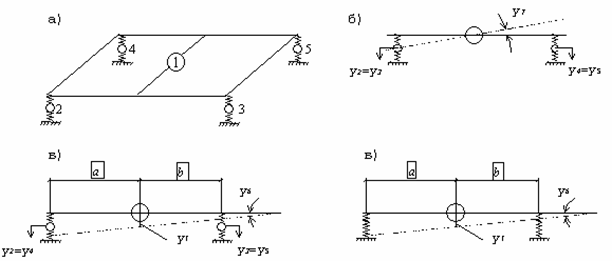
Рис. 32
В соответствии с этим продольные колебания описываются четырьмя, а поперечные колебания - тремя дифференциальными уравнениями.
Рассмотрим продольные колебания, которые имеют основное значение.
Обозначим
жесткости шин через С; жесткости передних и задних рессор через СП и
СЗ соответственно; массы кузова и колеса - через m и mК. Радиус инерции кузова относительно поперечной оси,
проходящей через его центр тяжести, обозначим через ![]() .
.
Тогда деформации рессор составляют
![]() (передняя рессора);
(передняя рессора);
![]() (задняя
рессора).
(задняя
рессора).
Уравнения движения составим на основе уравнений Лагранжа.
Кинетическая энергия системы складывается из следующих частей:
кинетической энергии кузова
![]() ;
;
кинетической энергии передних колес
![]() ;
;
кинетической энергии задних колес
![]() .
.
Суммарная кинетическая энергия:
![]() .
.
Потенциальная энергия деформации рессор:
![]() .
.
Потенциальная энергия сжатия шин:
![]() .
.
Суммарная потенциальная энергия:
![]() .
.
Вычисляя соответствующие производные и подставляя в уравнения Лагранжа (29), получим
 (73)
(73)
Частное
решение системы (73) имеет вид
![]()
Подстановка частного
решения в уравнение (73) приведет, как в рассмотренных ранее системах, к
однородным относительно амплитуд ![]() алгебраическим
уравнениям и соответственно обнаружатся четыре собственных частоты колебаний.
алгебраическим
уравнениям и соответственно обнаружатся четыре собственных частоты колебаний.
С практической точки зрения удовлетворительный результат дает рассмотрение упрощенной схемы продольных колебаний (рис. 32,г).
Будем считать
шины недеформируемыми, тогда рассматриваемая система обладает двумя степенями
свободы, соответствующими координатам ![]() . Положим в полученных выше выражениях для кинетической и
потенциальной энергий
. Положим в полученных выше выражениях для кинетической и
потенциальной энергий ![]() , тогда эти выражения принимают вид
, тогда эти выражения принимают вид
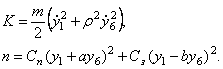
Уравнения
Лагранжа:
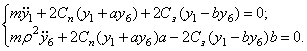
Частное
решение
![]()
После его подстановки
получим
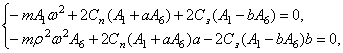
или
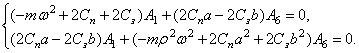 (74)
(74)
Как обычно, для получения нетривиального решения приравниваем нулю определитель системы:
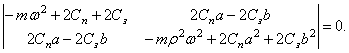
Раскрывая определитель, получим частотное уравнение в виде
![]() (75)
(75)
Определив из уравнения (75) собственные частоты, можно найти соответствующие им собственные формы колебаний. Для этого из какого-либо (например, из первого) уравнения системы (74) нужно образовать отношение амплитуд
![]() (76)
(76)
и подставить в него поочередно оба корня частотного уравнения.
Рассмотрим
подробно частный случай такого распределения масс, при котором ![]() В этом случае частотное
уравнение (75) имеет корни:
В этом случае частотное
уравнение (75) имеет корни:
 (77)
(77)
Для
определения собственных форм колебаний подставим эти корни поочередно в
соотношение (76). Тогда для первой собственной формы получим
![]()
а для второй
собственной формы - ![]()
Эти формы колебаний представлены на рис. 33,а,б. Их особенностью является неподвижность одной оси автомобиля при колебаниях другой. Формулы (77) показывают, что в этом частном случае частоты можно вычислять, используя схему, показанную на рис.33,в, т.е. распределяя общую массу по закону рычага.
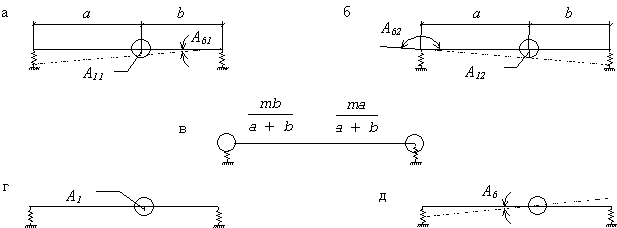
Рис. 33
В другом частном случае, когда Спа = СЗb, уравнения (74) становятся независимыми
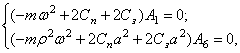 (78)
(78)
что означает
возможность чисто вертикальных колебаний при отсутствии поворотов -
«подпрыгивание» (рис. 33,г), а также чисто угловых колебаний при неподвижности
центра тяжести - «галопирование» (рис. 33,д). Действительно, система (78) удовлетворяется
решением ![]() при выполнении
равенства
при выполнении
равенства
![]() (79)
(79)
и решением ![]() при выполнении
равенства
при выполнении
равенства
![]() (80)
(80)
Из (79) находим первую собственную частоту:
![]() ,
,
а из (80) - вторую собственную частоту:
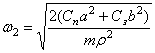 .
.
Пример 11. Определить собственные частоты
и собственные формы колебаний автомобиля, для которого известно: ![]()
![]()
Решение
Частотное уравнение (75) после подстановки в него заданных числовых значений принимает вид
![]()
Собственные
частоты:
![]()
Для определения собственных форм колебаний воспользуемся формулой (76)

Собственные формы колебаний представлены на рис. 34,а,б.
Рис. 34
Первая форма представляет собой, в основном, «подпрыгивание» кузова, а вторая - «галопирование».
Убедимся в
ортогональности этих форм. Условие ортогональности имеет вид
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Сопротивление материалов
Прикладная механика Строительная механика Теория машин и механизмов
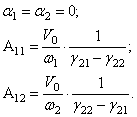
 .
.