Главная
Раздел 1. Основные понятия
и определения
1.1. Способы образования механических моделей с конечным числом степеней свободы
Числом степеней свободы механической системы называется число независимых координат, однозначно определяющих положение всех её материальных точек. В задачах динамики положение точек системы меняется с течением времени, следовательно, координаты точек являются функциями времени.
Основная задача динамики состоит в определении этих функций или, как говорят, в определении движения системы. После этого по известным формулам сопротивления материалов определяются внутренние усилия, напряжения и деформации в элементах колеблющегося тела.
Любая реальная механическая система состоит из бесконечного числа материальных точек, связи между которыми не являются абсолютно жёсткими, поэтому число степеней свободы реальной механической системы бесконечно велико. Решение задачи о колебаниях таких систем представляет собой весьма сложную проблему. Получить точное аналитическое решение, как правило, невозможно, а часто и нецелесообразно, поэтому при переходе от реального объекта исследования к расчётной схеме приходится вводить упрощения, связанные с ограничением числа степеней свободы системы.
Можно указать три основных способа образования механических моделей с конечным числом степеней свободы системы.
Первый способ состоит в том, что относительно менее массивные части системы полагаются совсем невесомыми элементами (при этом они могут считаться как жёсткими, так и деформируемыми), а наиболее массивные части принимаются за абсолютно твёрдые тела, которые, в случае их сравнительно небольших размеров, считаются материальными точками.
Например, пружина (рис. 1,а) и балка (рис. 1,б) считаются безмассовыми и упругими, а полосы (рис. 1,в) - безмассовыми и жёсткими. В качестве обобщённой координаты приняты горизонтальное (рис. 1,а) и вертикальное (рис. 1,б,в) перемещения. Все указанные модели представляют собой системы с одной степенью свободы.
Рис. 1
Аналогичным образом можно образовывать модели с любым конечным числом степеней свободы.
Второй способ состоит в том, что распределённые по всему объёму системы свойства податливости сосредотачиваются в конечном числе точек или линий. При этом система представляется в виде совокупности упруго- сочленённых жёстких элементов.
Например, упругая балка с непрерывно распределённой массой может быть приближённо заменена рядом жёстких звеньев, соединённых упругими шарнирами, количество которых определяется требуемым уровнем точности решения задачи (рис.2).
Рис. 2
Третий способ основан на некоторых предположениях об изменении конфигурации системы в процессе колебаний.
Например, для системы грузов, соединённых пружинами (рис. 3) можно
принять, что отношение между перемещениями 
неизменны во времени,
а отношение 
заранее назначается.
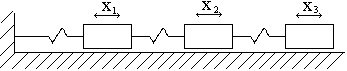
Рис. 3
В результате
движение системы полностью описывается одной функцией времени, например 
, через которую выражаются перемещения всех точек системы.
Таким образом, реальный объект приведён к механической модели с одной степенью
свободы.
По этому же способу для балки на двух опорах можно принять, что форма изогнутой оси остается неизменной в любой момент, а изменяется только её масштаб. Тогда вертикальное перемещение точек балки при её колебаниях, представляющее собой функцию двух переменных, можно представить в виде
где f(x) -постоянная функция формы, а q(t) -переменная функция времени, являющаяся единственной неизвестной величиной задачи. Одна и та же реальная механическая система может быть приведена к модели с одной или несколькими степенями свободы любым из трёх перечисленных способов.
1.2. Классификация сил, действующих при колебаниях
При определённых допущениях все разнообразные по своей природе внешние и внутренние силы, действующие в колеблющейся системе, можно разделить на несколько характерных групп.
Обобщенные вынуждающие (возмущающие) силы - это внешние силы, являющиеся заданными функциями времени, не зависящие от движения системы, но влияющие на него. Причины возникновения этих сил весьма разнообразны. Например, при работе электродвигателя, установленного на балке или на каком-либо фундаменте, вследствие неуравновешенности ротора возникает центробежная сила инерции, вертикальная составляющая которой вызывает колебания опорной конструкции. Этот вид возбуждения колебаний называется инерционным. Возможны другие причины возникновения вынуждающих сил, например, периодические изменения давления в цилиндрах двигателей внутреннего сгорания или периодические изменения сил притяжения электромагнитов, питаемых источником переменного тока.
Все перечисленные случаи представляют собой силовое
возбуждение вынужденных колебаний. В некоторых случаях возбуждение колебаний
задаётся кинематически, например автомобиль,
движущийся по неровной дороге. Такое возбуждение всегда можно заменить
эквивалентным силовым возбуждением.
Весьма разнообразны законы изменения возмущающих сил во времени. Наиболее часто встречаются периодические вынуждающие силы. Особую роль здесь играет гармоническая вынуждающая сила, т.е. сила, которая изменяется во времени по закону синуса или косинуса. Такая сила возникает при работе машин с равномерно вращающимися роторами. Машины с кривошипо-шатунными механизмами также вызывают появление периодической возмущающей силы, которая, однако, не является гармонической.
Возможны также колебания, обусловленные действием непериодических вынуждающих сил, представляющих собой случайные функции времени - случайные процессы. К последним относится, например, уже упоминавшееся воздействие неровной дороги на движущийся автомобиль.
Обобщенные позиционные силы - это силы, зависящие от положения точек системы, т.е. от обобщенных координат. Особое значение здесь имеют восстанавливающие силы, которые возникают при отклонении системы от положения равновесия. Эти силы обусловливают способность системы совершать свободные колебания. Основным типом восстанавливающих сил являются силы упругости. В простейшем случае линейно деформируемой системы восстанавливающая сила упругости пропорциональна отклонению системы. Свойства упругих связей при этом определяются коэффициентом жесткости, который представляет собой обобщенную силу, способную вызвать обобщенное единичное перемещение. Возможны случаи, когда между силой и отклонением существует нелинейная зависимость. При этом упругие свойства связей невозможно определить одним коэффициентом и приходится использовать так называемую упругую характеристику, уравнение которой F=F(x) иллюстрируется графиком в координатах x, F. Упругая характеристика строится расчетным путём или экспериментально.
Наряду с силами упругости восстанавливающими свойствами обладают также сила плавучести и в определенных случаях сила тяжести.
Обобщенные силы трения зависят от
обобщенных скоростей и направлены противоположно движению. Эти силы совершают
необратимую работу, что приводит к диссипации (рассеянию) механической энергии,
поэтому иногда их называют диссипативными
силами. Обычно силы трения препятствуют движению; исключение составляют
автоколебательные системы. Диссипативные свойства описываются при помощи характеристик трения, которые представляют собой
графические зависимости вида 
. В ряде случаев характеристика трения может быть
нелинейной или разрывной.
Силы смешанного характера могут
развиваться в сложных механических системах. Характерной особенностью таких сил
является принципиальная невозможность их разложения на вышеперечисленные
составляющие типа F(t) , F(x) , F(
). В качестве примера рассмотрим параметрическую
систему - маятник, на который действует вертикальная сила 
(рис. 4). Момент
внешних сил относительно оси шарнира равен сумме моментов силы веса mg и силы F:
.
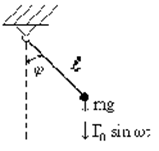
Рис. 4
Этот
восстанавливающий момент M
зависит не только от смещения 
, но и от времени t, причём выражение
нельзя представить в
виде суммы 
, т.е. невозможно выделить восстанавливающую и возмущающую
составляющие общего момента. В автоколебательных системах возможно действие сил
вида 
, также неразложимых на элементарные составляющие типа F(x) и 
.
1.3. Классификация колебаний
Все многообразие окружающих нас колебательных процессов можно классифицировать по ряду характерных признаков.
В соответствии с законом, по которому величина, характеризующая колебательный процесс, изменяется во времени, различают периодические и непериодические колебания.
Периодические колебания подчиняются закону:
f(t + T)=f(t),
где величина T называется периодом колебаний. Кроме того, имеется широкий промежуточный класс почти периодических колебаний, для которых
,
где 
- почти период, а 
- сколь угодно малая величина.
Простейшими и в то же время наиболее часто встречающимися являются гармонические колебания (рис.5), которые описываются уравнением
,
где А - амплитуда
колебаний; 
- круговая (или
циклическая, или угловая) частота; 
- фаза колебаний; 
- сдвиг фазы;
величина, обратная периоду колебаний, называется секундной частотой и измеряется в герцах:
.
1 Гц соответствует одному циклу изменения за 1 с.
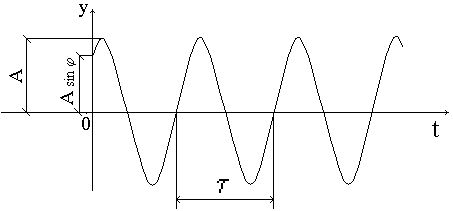
Рис. 5
Часто встречаются периодические, но негармонические колебания (рис. 6). Их всегда можно рассматривать как сумму простых гармонических колебаний. Процесс разложения периодических негармонических колебаний на простые гармонические составляющие (гармоники) называется гармоническим анализом и выполняется при помощи рядов Фурье.
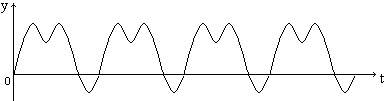
Рис. 6
Кроме того, часто встречаются следующие виды колебаний: затухающие (рис. 7,а), нарастающие (рис. 7,б), биения (рис. 7,в).
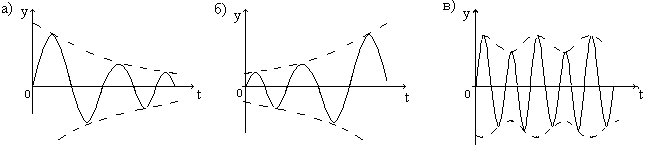
Рис. 7
Все рассмотренные (рис.7) виды колебаний происходят с постоянной частотой при монотонном изменении амплитуды. Возможны также колебания с переменной частотой и постоянной амплитудой или переменными частотой и амплитудой.
Колебания могут происходить относительно нулевого отсчетного уровня, смещённого и переменного.
По способу возбуждения различают 4 типа
колебаний: свободные, вынужденные ,
параметрические и автоколебания.
Свободными (или собственными) называются колебания, возникающие в изолированной системе вследствие внешнего возбуждения, вызывающего у точек системы начальное отклонение от положения равновесия, и продолжающиеся затем благодаря наличию упругих внутренних сил, восстанавливающих равновесие.
Вынужденными называются колебания упругой системы, происходящие при действии на неё в течение всего процесса колебаний внешних периодически изменяющихся вынуждающих сил.
Параметрическими называются такие колебания упругой системы, в процессе которых периодически изменяются физические параметры систе-
мы - величины, характеризующие её массу или жесткость.
Автоколебаниями упругой системы называются незатухающие колебания, поддерживаемые такими внешними силами, характер взаимодействия которых определяется самим колебательным процессом.
Классификацию колебаний проводят также по виду деформации, возникающей в элементах колеблющейся системы. В частности, применительно к стержневым системам различают продольные, поперечные (изгибные) и крутильные колебания.
1.4. Методы получения дифференциальных уравнений движения
Можно выделить 3 способа составления уравнений движения. Наиболее общей формой таких уравнений являются уравнения Лагранжа:
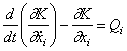( i =
1,2,...,n), (1)
где К - кинематическая энергия системы, t - время; 
- обобщённые координаты; 
- обобщенные скорости; 
- обобщенная сила; n - число степеней свободы системы.
Для системы с конечным числом степеней свободы из уравнений (1) можно получить важные соотношения частотного характера, которые удобны при исследовании колебательных систем определенных типов.
Так, в задачах
о свободных колебаниях упругих систем без трения обобщенные силы выражаются через
потенциальную энергию системы П в виде
( i = 1,2,...,n). (2)
При этом уравнения Лагранжа принимают вид
( i =
1,2,...,n). (3)
Прямой способ. По этому способу из системы (рис. 8,а) мысленно выделяются сосредоточенные массы, и каждая из них рассматривается как свободная материальная точка, находящаяся под действием позиционных восстанавливающих сил, которые выражаются через выбранные обобщенные координаты (рис. 8,б); для каждой точки записывается соответствующее дифференциальное уравнение движения.
Обратный способ. Здесь после отделения сосредоточенных масс рассматривается оставшаяся безынерционная система жёстких и упругих связей (так называемый безмассовый скелет), которая находится под действием кинетических реакций (сил инерции) отделённых частей системы, причём эти силы инерции выражаются через обобщённые ускорения (рис. 8,в). Для безмассового (безынерционного) скелета системы формируются статические соотношения.
При анализе свободных колебаний некоторых консервативных систем с одной степенью свободы удобно применять энергетический способ, который основан на законе сохранения энергии, согласно которому, сумма кинетической и потенциальной энергий системы в процессе колебаний остается неизменной.
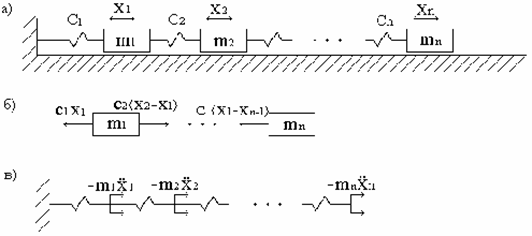
Рис. 8
email: KarimovI@rambler.ru
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
Теоретическая механика Сопротивление материалов
Прикладная механика Строительная механика Теория машин и механизмов
